이번 글에서는 수집된 데이터를 이용하여 간단한 EDA와 전처리 그리고 Feature engineering을 진행해 볼 것이다.
1. EDA
우선 EDA의 시작이라고 하는 데이터 정보부터 확인해 봤다.(따로 수정하지 않고 그대로 코드를 사용했다면 나와 동일한 상태일 것이기 때문에 내 기준으로 설명하겠다.) 나는 잠수교, 청담대교, 한강대교, 행주대교 외에 광진교, 팔당대교, 중랑교, 전류리의 수위를 수집하였는데 수집한 이유는 이후에 나온다.
1-1. 데이터 확인
column과 info를 찍어보면 다음과 같다.


wl=수위, fw=유량, rf=강수량, swl=팔당댐수위, inf=팔당댐유입량, sfw=팔당댐저수량, ecpc=팔당댐공용량, tototf=팔당댐방출량을 나타낸다.
총 25개의 칼럼을 가지고 있으며, 결측치가 다수 존재하는 칼럼도 보이고, 사실 확인해 보면 nan으로 카운트가 안 돼있는 것들 중 nan이라는 글씨가 박혀있는 것도 있고 해서 결측치를 추후 처리해줘야 한다.
당연하게도 수위값이 Target이기 때문에 수위에 대한 분포를 확인해 보았다.
타깃값인 잠수교, 청담대교, 한강대교, 행주대교의 수위를 연도별로 구분하여 확인해 봤는데 중간중간 튀는 값들이 있으나 각각의 대교에서도 연도별로 패턴이 비슷한 걸로 보였고, 4개의 대교가 거의 동일한 수위 분포를 가지고 있었다.
1-2. 수위 데이터 확인
1-2-1. 연도별 수위

다음으로 특정 기간을 바꿔가며 대교들의 수위 변화를 확인하였다.
각 대교별로 수위의 스케일이 다르기 때문에 각 대교별로 수위를 0~1로 정규화를 하여 추세만 비교하고자 하였다.
1-2-2. 정규화된 수위 추세

위 그림에서 청담대교->잠수교->한강대교->행주대교 순으로 수위가 변하는 것을 볼 수 있는데 이것은 당연한 결과이며 데이터가 제대로 되었다는 것을 볼 수 있다.
이해를 돕기 위해 잠시 실제 대교들의 위치를 보고 넘어가자.(강화대교와 전류리는 실제로는 더 좌측에 있습니다.)
1-2-3. 실제 관측 지점

보면 왜 데이콘에서 송정동, 대곡교, 진관교의 강수량을 줬는지 알 수 있고(한강의 인근 지역이기 때문),
방금 위에서 본 수위의 변화 추세가 대교들이 위치한 장소의 순서와 동일하다. 또한 그렇기 때문에 내가 중랑교, 팔당대교, 전류리, 중랑교의 수위를 추가적으로 수집하였다.
1-2-4. 홍수기와 갈수기 수위 비교
우선 홍수기란 법령으로 지정된 기간으로 6월 21일~9월 20일을 홍수기라고 지정하였고, 그 외를 갈수기라고 한다.

이 기간에 따라 수위가 차이가 날 것이라 생각하여, 홍수기와 갈수기의 평균 수위를 비교해 보았다.
이미지 보기-펼치기
한눈에 볼 수 있듯이 모든 대교에서 매년 홍수기의 평균 수위가 비홍수기보다 높은 것을 확인할 수 있었고, 이에 이러한 정보를 추후에 사용하고자 하였다.
1-3. EDA 정리
여기까지 아주 간단하게 데이터를 살펴봤는데, 우선 4개의 대교+추가적으로 수집한 대교들의 수위가 매우 연관성이 높으며 수위라는 것 자체가 흐름이 있는 것을 확인하였으며, 홍수기와 갈수기의 수위 차이도 확인하였고 전체적인 데이터 분포들도 비슷한 것을 확인하였다.
2. 전처리
이제 데이터 전처리를 진행해 볼 것인데, 우선 데이터 전처리로는 데이터 결측치 제거 및 이상치 제거, 필요 없는 column을 제거하였다.
2-1. 이상치 제거
이상치 제거는 학습에 방해가 되는 데이터들을 제거하기 때문에 매우 중요한 과정이다.
따라서 다양한 방법을 진행해 봤었으나, 결과는 그냥 눈으로 보면서 결측치를 제거하는 것이었다.
우선은 IQR을 이용한 결측치처리, 'winsorize` 기법을 사용했었었다.
IQR은 널리 알려져 있듯이 사분위수를 이용하여 범위 바깥의 값들을 결측치로 처리하는 것이고, Winsorize는 데이터의 양 극단값들을 데이터의 최댓값으로 바꾸는 기법이다.
위의 두 가지 방법 모두 진행해 봤는데 이를 통해 탐지되는 이상치들은 사실 이상치가 아니라 실제로 홍수가 난 날이거나, 진짜로 수위가 높았던 날들이었다. 이들을 제거하고 모델 학습까지 진행하였더니 갈수기들은 대부분 수위 변화 폭이 크지 않고 높지 않기 때문에 그럭저럭 예측했던 반면 홍수기의 갑작스러운 수위변화들을 포착하지 못하였고 예측 결과의 max가 정해져 버렸다. (특정 수위 위로 다 잘린 듯한 결과가 예측되었다.)
따라서 그냥 무식한 방법일 수도 있지만, 데이터의 분포를 그려가며 10분 만에 수위가 비정상적으로 높아지거나 수위가 음수인 그런 눈에 보이는 데이터들만 모두 nan으로 채워줬다.
-> 사실 데이터가 10년 치로 많았기 때문에 이런 것들만 제거해 줘도 성능이 나와줬다. 아래는 잠수교 수위 예시이다
(좌측 전처리 전 / 우측 전처리 후)
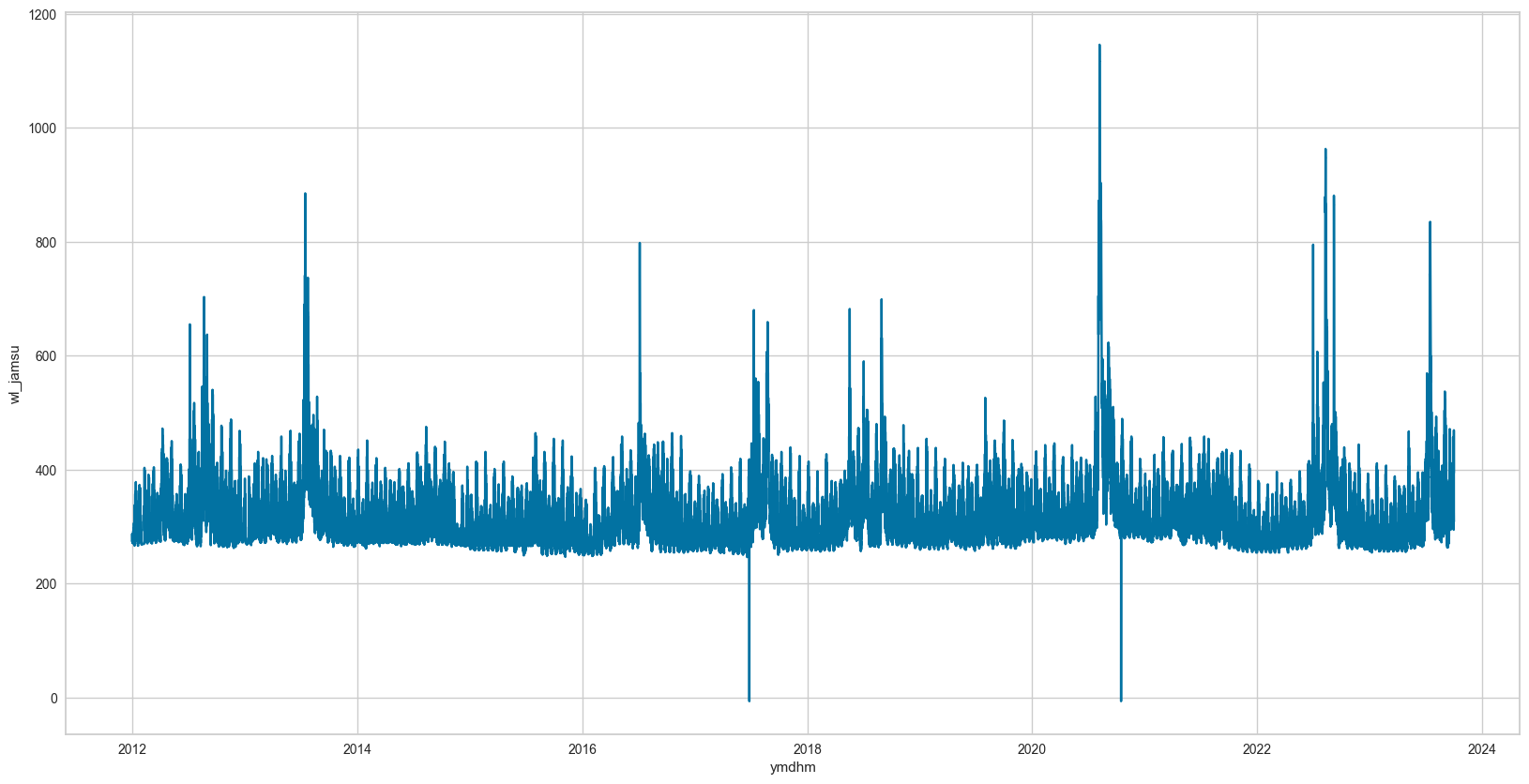
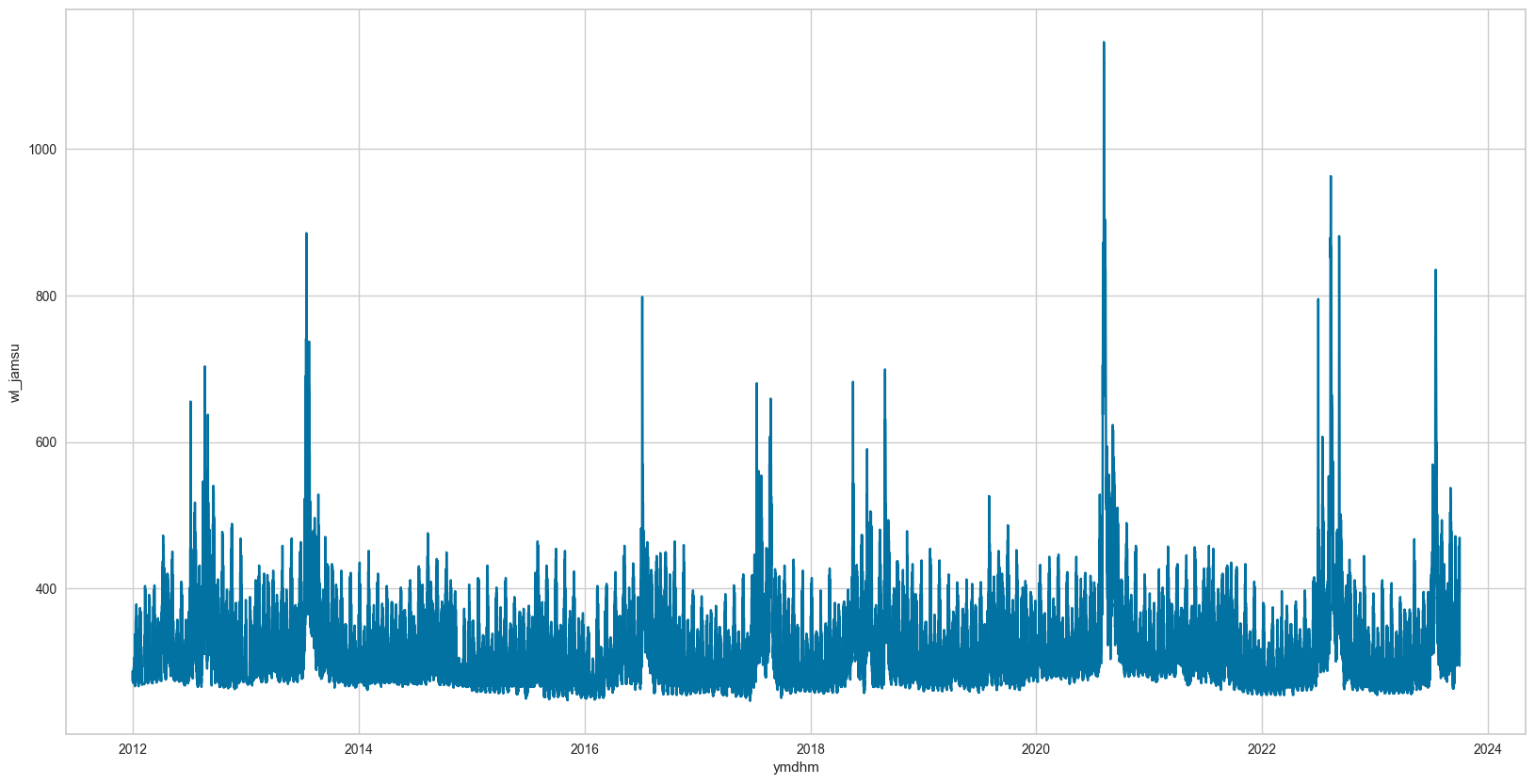
아쉬웠던 점은 나중에 알게 된 알고리즘이지만, Isolation Forest라는 이상치 탐지 알고리즘이 있는데 이걸 써볼걸 그랬다. 사실 이걸 쓴다고 크게 달라지진 않았겠지만 막일로 찾는 것은 데이터가 더 많아지거나 칼럼이 많아지면 적용이 불가능하기 때문에 나중에 시간 되면 Isolation Forest도 적용해 봐야겠다.
Isolation Forest를 통한 이상탐지 모델
Anomaly Detection(이상 탐지)
john-analyst.medium.com
위와 같이 모든 칼럼을 직접 확인하며 이상치들을 제거해 줬으며, 거의 대부분의 값이 0 혹은 nan이었던 잠수교와 전류리의 유량만 drop 해줬다.
2-2. 결측치 처리
기존의 결측치들과 위에서 이상치들을 모두 nan으로 채워줬기 때문에 결측치가 많이 존재하였다.
이 결측치를 채우는 방법도 다양한 방법을 시도해 봤는데 간단하게 설명해 보겠다.
평균: 가장 간단한 방법으로 그냥 df.fillna(df.mean())으로 평균을 이용하여 결측값을 채우는 방법도 있다. -> 수위의 변동이 격차가 큰 부분들이 포함되어 있어 적절하지 않다고 생각
ffill, bfill: 결측값의 앞이나 뒤의 값으로 채우는 방식이다. -> 결측치가 연속적으로 존재하여 사용하지 않았음.
interpolate:
보간법을 실행하는 함수로, 보간법이란 아래와 같이 주어진 관측값들 사이의 결측값을 예측하는 방식이다.(반대 보외법)
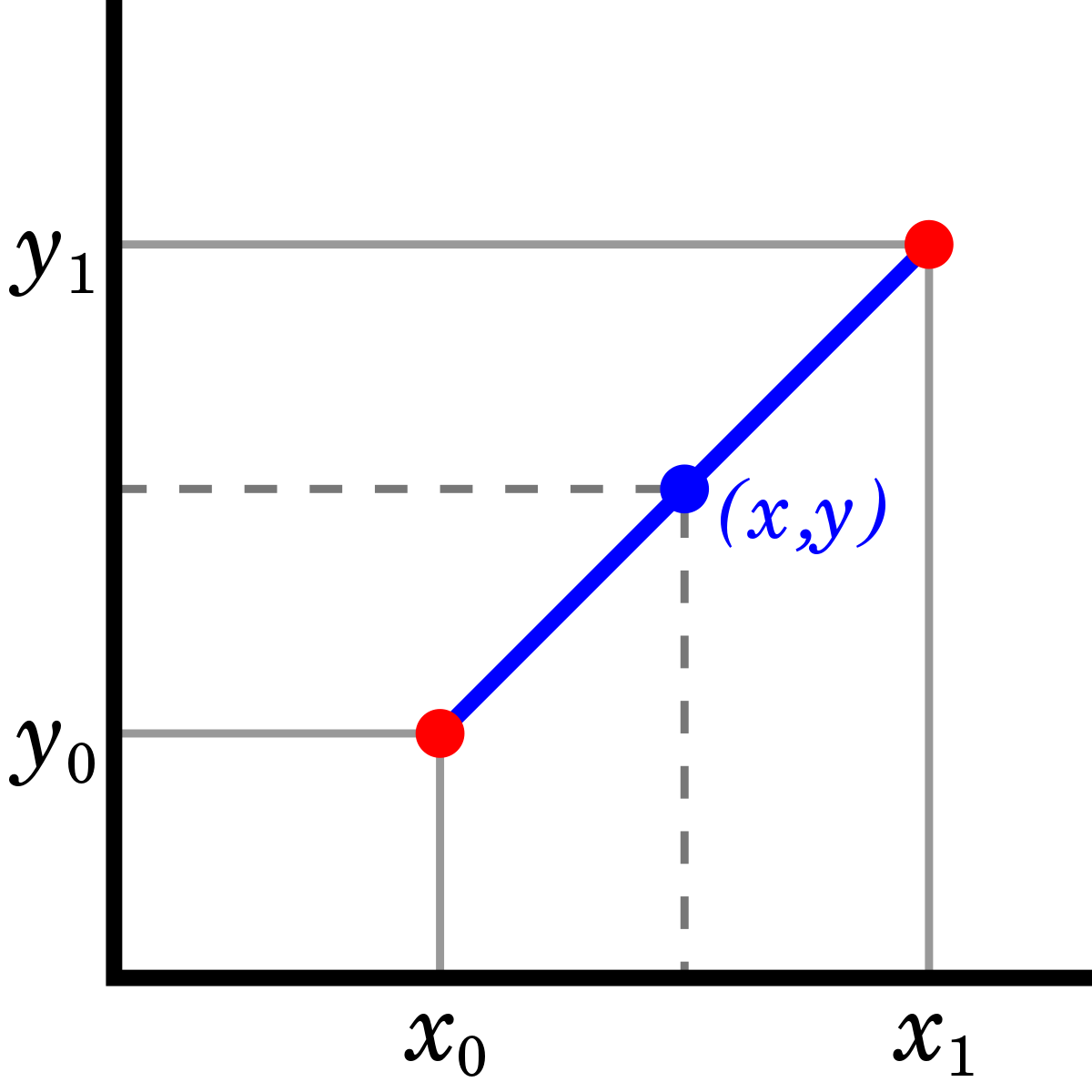
이 보간법도 자세히 파고들면 선형보간, 스플라인 보간법 등 다양하게 있는데 내가 관심 있게 본건 2개 선형보간법과 시간을 기반으로 한 보간법이다.
우선 interpolate(method='time')과 interpolate(method='linear')로 나뉘는데 간단한 예시로 비교해 보자.
method='time'의 경우 datetime인덱스에서만 작동하는데 시간간격을 고려하여 결측치를 보간한다.
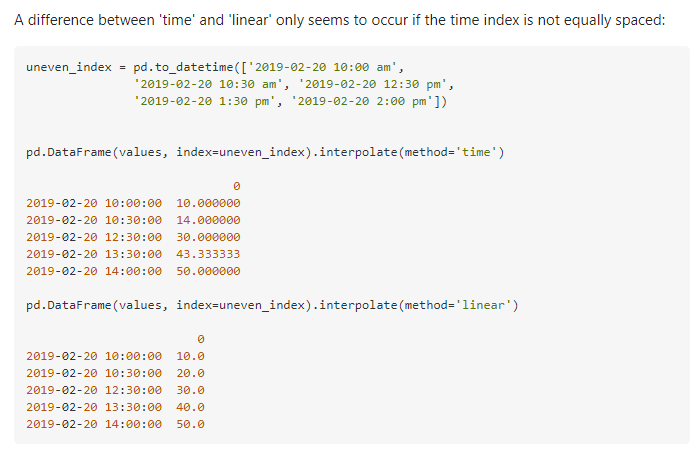
그러나 이 방법은 train 데이터에서는 사용해도 되지만 대회 규칙상 데이터의 결측치를 채울 때 미래의 데이터를 사용하여 채우면 안 되기 때문에 즉 test 데이터에서는 보법을 이용하여 결측치를 채우면 안 되기 때문에 다른 방법을 사용하고자 했다.
여기까지가 내가 시도했던 방법들이고 다른 사람들의 코드들을 참조해 봤을 때 mlp나 LGBM등을 이용한 결측치 처리 등이 있었던 것 같다. 나는 최종적으로 아래의 이동평균을 이용하여 결측치를 처리하였다.
2-2-1. 이동평균 결측치 처리
내가 사용한 이동평균을 이용한 처리만 확인해 보겠다.
# 아래의 방식으로 이동평균 결측치를 채우려했으나, 연속된 nan에서 제대로 작동하지 않음 ->틀린코드
#for column in data.columns:
# data[column] = data[column].fillna(data[column].rolling(window=window_size, min_periods=1).mean())
#data.info()
for col in data.columns[1:]:
indices = data[pd.isnull(data[col])].index
col_num = np.where(data.columns == col)[0][0]
print(f"{col}s NaN count:", len(indices))
for idx in tqdm(indices):
data.iloc[idx, col_num] = np.mean(data[col][(idx-window_size):idx])
data.info()코드는 위와 같이 각 칼럼별로 순회하면서 결측치가 있는 위치를 찾고, 해당 결측치를 이전 n개만큼의 평균으로 대체한다.
기존에 위의 코드 말고 이동평균 함수를 이용하여 결측치를 채우려고 했는데 위처럼 반복문으로 도는 게 아니라 이동평균을 이용하여 하면 연속된 결측치들이 채워지지 않아서 하나하나 반복하며 결측치를 채우고 그 채운 결측치를 이용하여 또 채우고 이런 식으로 반복하였다.
여기까지 하면 모든 이상치 및 결측치 처리가 끝이 났다.
3. Feature engineering
우선 이전에 eda에서 확인하였듯이 수위는 물의 흐름이기 때문에 이전값들에 영향을 많이 받을 것이고 홍수기 갈수기 등을 확인하였을 때 시간적인 영향도 많이 받는다는 것을 확인할 수 있었다.
그래서 총 2가지의 feature engineering을 진행했다.
3-1. 차분
차분이란, 연이은 관측값들의 차이를 계산하는 것을 의미한다. 보통 시계열 데이터에서 정상성과 같이 자주 등장하는 단어이다. 나는 타깃 대교 4개의 차분 값을 나타내는 칼럼을 추가해 줬다. 즉 10분간 수위 변화량을 추가해 준 것이다.
# 각 대교 10분간 수위 변화량 - 차분값
data['wl_jamsu_rate'] = data['wl_jamsu'].diff()
data['wl_cheongdam_rate'] = data['wl_cheongdam'].diff()
data['wl_hangang_rate'] = data['wl_hangang'].diff()
data['wl_haengju_rate'] = data['wl_haengju'].diff()3-2. 시간 관련 변수 추가
우선 기본적으로 시간과 월을 추출해 줬으며, 추가적으로 이 시간과 월을 모두 주기성을 갖도록 변환해 줬다.
주기성을 갖는다는 게 무슨 말이냐. 그냥 월과 시간을 추출하기만 하면 그 값들은 단순 1,2,3,~12 이렇게 정수형태로 들어간다. 그럼 1월과 12월은 비슷함에도 불구하고 가장 멀리 떨어져 있게 된다.
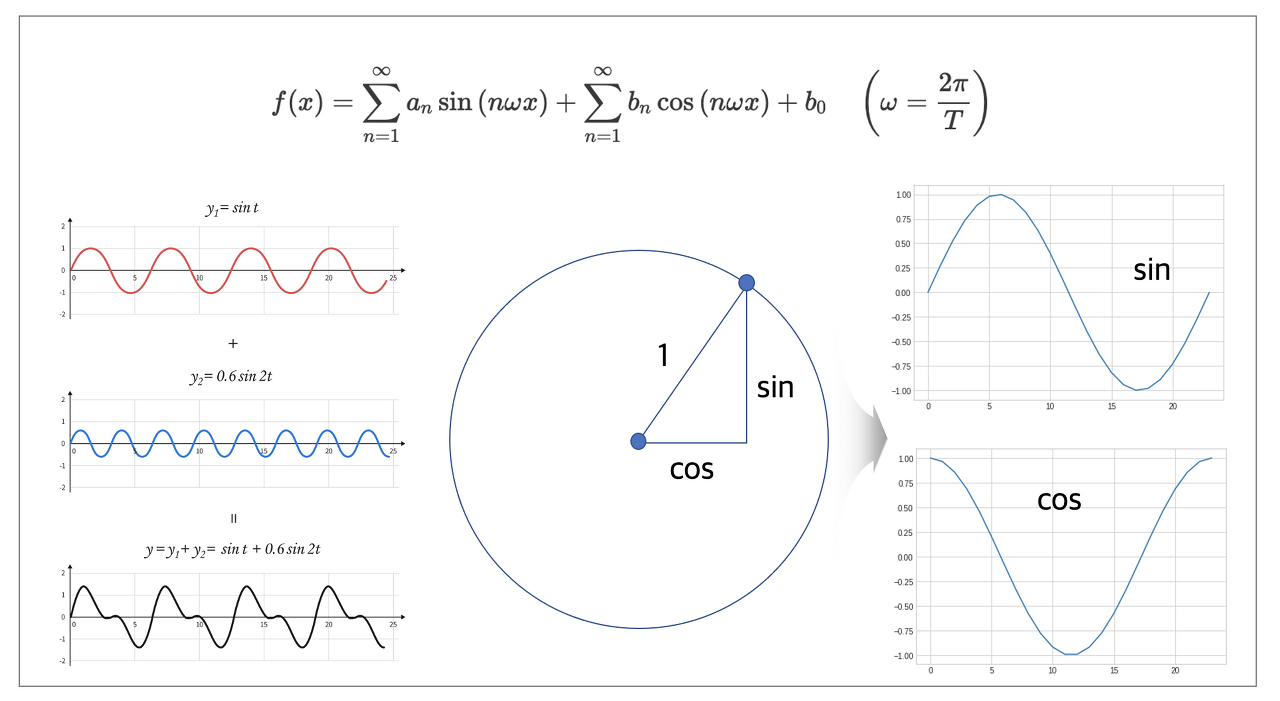
이는 푸리에 특징이라고 한다는데, 사실 위에처럼 무슨 말인지는 이해했는데 수학적으로는 잘 모르겠다.
아무튼 시간과 월을 푸리에 특징 즉 sin과 cos으로 이루어지도록 구성한다.
자세한 시간의 주기성을 변환하는 것은 아래 블로그를 참조하면 좋을 것 같다.
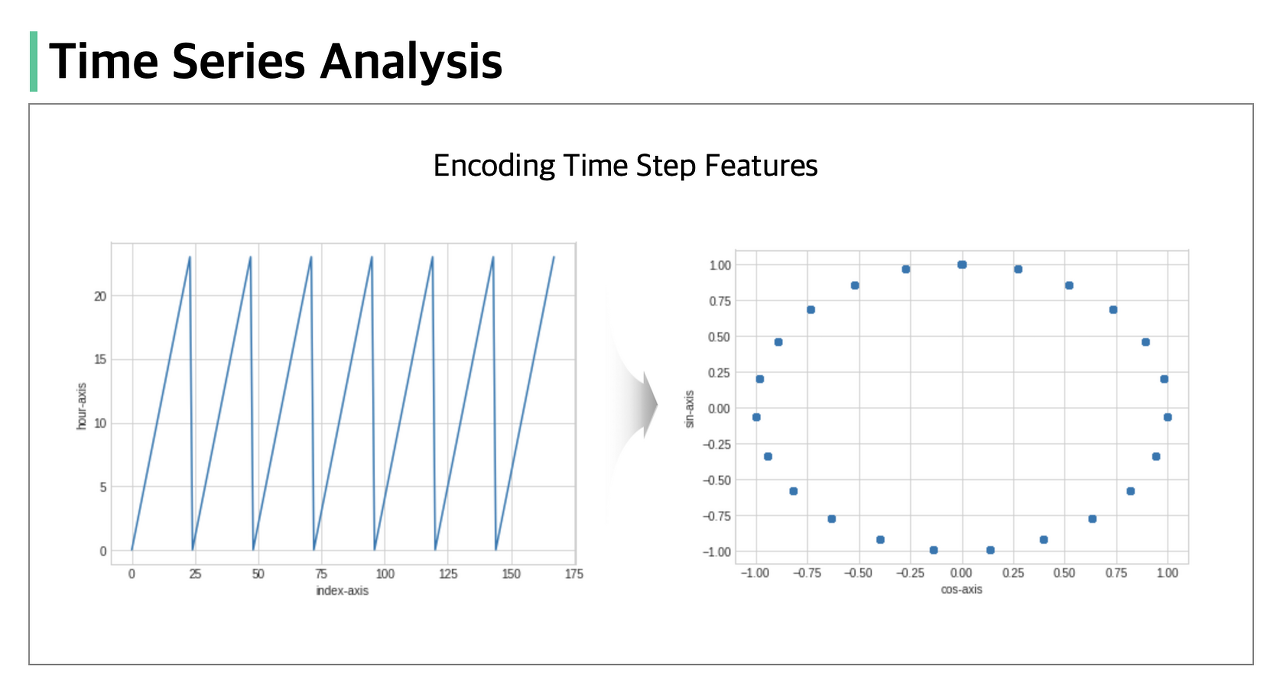
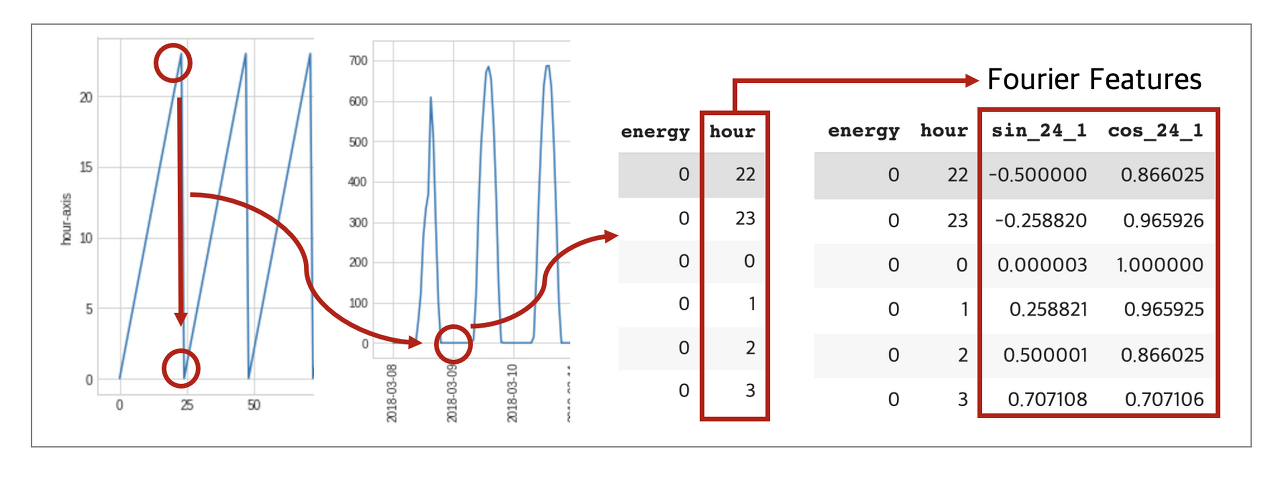
시계열 데이터 전처리(Encoding Time Step Features)
시계열 데이터를 분석하는 과정에서 주기적 성질을 지니고 있는 데이터들을 빈번히 발견할 수 있습니다. 데이터가 주기적 성질을 지니고 있다면 사인함수, 코사인함수와 같은 삼각함수의 합으
today-1.tistory.com
4. EDA, 전처리, Feature engineering 후기
우선 내가 사용한 방법들은 위와 같다.
실제로 적용하게 된 건 별로 없지만 각종 방법들을 시도하고 모델링까지 진행하는 실험을 해가며 방법을 선택하느라 시간이 좀 많이 걸렸다.
다른 분들 코드도 많이 참조하였는데, 이동평균을 칼럼으로 추가한 사람들도 있었고, n분전 수위값을 칼럼으로 추가하고 푸리에변환, STL 분해, 기온 일사량 일조량 추가, 등등 다양한 feature engineering을 한 것들도 참고해 보면 좋을 것 같다.
참고 내용
[팀명 또도박사, 1th Private Leader Board: 0.78892 방법론]
팔당댐 홍수 안전운영에 따른 한강 수위예측 AI 경진대회
dacon.io
[ML Study 2022] 7주차
competition팔당댐 홍수 안전운영에 따른 한강 수위예측 AI 경진대회ThemeTime Series RegressionmetricRMSENotes팔당댐 유입량, 저수량, 공용량 등의 데이터를 바탕으로 6월 1일 00시부터 7월 18일 23:50분까지의
velog.io
팔당댐 수위 예측 AI 대회 코드 #3 EDA실행
대회측에서 제공해준 강수량 데이터와 물 데이터를 먼저 합쳐준다(rf_df와 water_df는 2-1에서 수정해둔 그 상태 그대로 이용)1편에서 가공해둔 외부 데이터 (gimpo_seoul_namyang.csv)를 불러내여 df에 합쳐
velog.io
GitHub - Im-GwangMuk/-Dacon-Hangang-Riv-7th-solution: This is the seventh place solution repository for competitions aimed at pr
This is the seventh place solution repository for competitions aimed at predicting the Han River's water level. - GitHub - Im-GwangMuk/-Dacon-Hangang-Riv-7th-solution: This is the seventh plac...
github.com
'프로젝트 > 수위 예측' 카테고리의 다른 글
| 선행시간에 따른 잠수교 수위 예측 (0) | 2024.01.10 |
|---|---|
| 한강 수위 예측 - 모델링 및 평가 (0) | 2023.12.15 |
| 한강 수위 예측 - 프로젝트 소개 및 데이터 수집 (1) | 2023.12.14 |
| 한강 수위 예측 - 프로젝트 시작 (0) | 2023.12.13 |

