퍼셉트론과 다층 퍼셉트론(MLP)

1. 인공신경망 ANN 

인공신경망 ANN: Artificial Neural Network는 인간의 뉴런을 이용한 자극 전달 방식을 본떠 만들어진 머신러닝 알고리즘이다. 뉴런의 시냅스(synapse)는 다른 뉴런으로부터 짧은 전기 신호를 받는 역할을 하고, 인간은 이 시냅스를 통하여 다른 뉴런으로부터의 자극을 전달하면서 학습하는데 이 과정을 본 따 이를 레이어(layer)과 퍼셉트론(perceptron)이라는 구조로 구현하여 만든 알고리즘이다. 현대의 딥러닝은 모두 이 ann으로부터 비롯된 neural network를 이용하여 만든 모델들을 통해 학습을 진행된다. 이러한 인공신경망에 사용되는 퍼셉트론에 대하여 먼저 알아보도록 하겠다. 

https://todayisbetterthanyesterday.tistory.com/42 / https://on-ai.tistory.com/3

https://ebrary.net/98123/economics/artificial_neural_networks

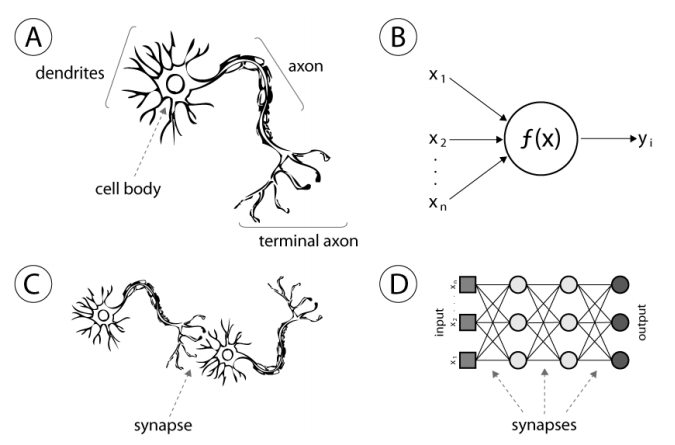
1-1.퍼셉트론(Perceptrons)

http://blog.quantylab.com/dl_hist.html

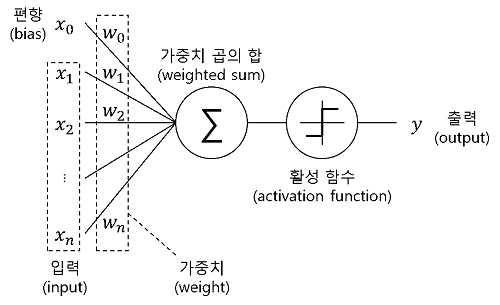
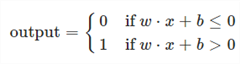
퍼셉트론은 노드와 엣지로 구성되어 있으며,  입력값에  Weight,가중치를 곱하고 bias를 더한 다음 활성화함수에 넣어 출력값을 1 혹은 0으로 정한다. 이 가중치와 임계값들을 업데이트해가며 학습을 진행한다.즉 모델의 학습이란, 주어진 입력에 대해 원하는 출력이 나오도록 weight와 bias를 업데이트하는 것을 의미한다. 

 위의 그림을 살펴보면 퍼셉트론은 입력값($ x_n $)에 가중치($ w_n $)에 bias를 더해서 활성화 함수에 넣어주는데 이때 bias,편향은 가중치를 조절하는 역할로 임계치를 넘거나, 못 넘도록 돕는다. 이러한 편향이 커질수록 대부분이 임계치를 넘기 때문에 모델이 단순화(과소적합)가 되고 편향이 낮을수록 학습데이터에만 너무 적합하게 되어 오버피팅이 일어날 수도 있다. 

보통 활성화함수(activation function)을 거치기 전의 최종 입력값을 $ z $라고 하는데, 수식으로 나타내면 다음과 같다. 

$$ z = w_1x_1 + w_2x_2 + \ldots + w_nx_n + b $$

이러한 퍼셉트론의 식을 간단하게 표현해보면 $ w_1x_1+w_2x_2+b $인데, 이 결괏값 z가 0보다 큰지 작은지에 따라 output이 결정되고 이는 선형분리를 의미한다. 이를 좌표계에 나타내면 아래 그림과 같다. 

위와 같이 퍼셉트론을 이용한 선형분리의 특성 때문에 초반에 많은 인기를 끌었는데, 왜냐하면 어떠한 연산식이든 AND, OR, NAND 등의 로직을 통해 구현이 가능하기 때문에 이러한 것을 퍼셉트론이 가능하게 한다는 점에 인기를 끌었다. 

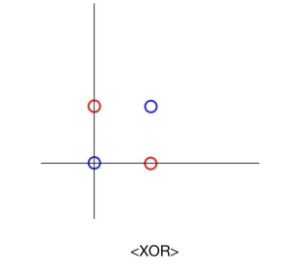
그러나 퍼셉트론 한 층으로는 XOR: 비선형분리가 불가능하였는데, 여러 층의 퍼셉트론을 이용하여 비선형분리까지 가능하다는 것이 증명되었다. 이것이 다층 퍼셉트론의 등장이다. 

AND 게이트는 두 입력이 모두 1일 때만 1을 출력하고 그 외는 0을 출력한다.

NAND 게이트는 두 입력이 모두 1일 때만 0을 출력하고 그 외는 1을 출력한다.

OR 게이트는 두 입력이 모두 0일 때만 0을 출력하고 그 외는 1을 출력한다.

XOR 게이트는 두 입력이 같으면 0 다르면 1을 출력한다. 

https://yhyun225.tistory.com/20

정리하자면 퍼셉트론이란 입력을 주면 정해진 규칙(가중치와 편향)에 따라 출력이 나오게 되는데 가중치와 편향을 조절하여 모델을 조정할 수 있다. 또한 이 퍼셉트론 1층을 이용하여 선형분리(AND, OR..)가 가능하며 2층으로 XOR 게이트도 구현 가능하다. 

1-2. 다층 퍼셉트론 (Multi-Layer Perceptron, MLP)

본래 퍼셉트론이란, 활성화함수를 계단함수로 사용하는 인공신경을 의미했었다. 그러나 MLP는 그저 어떤 활성화함수를 사용해도 신경망 구조로 되어있으면 MLP라고 부른다. 

다층 퍼셉트론은 이름에서 알다시피 여러층의 퍼셉트론을 쌓아 신경망 구조로 연결한 것을 의미한다. 

우선 `레이어(layer)`은 입력층, 은닉층, 출력층으로 구분되고, 은닉층 hidden layer가 1층이면 얕은 신경망, 여러 층이면 깊은 신경망으로 구분되기도 한다. 또한 일반적으로 은닉층의 개수+1 층의 MLP라고 부른다(ex 은닉층이 2개면, 2층 mlp)

2. 활성화함수(activation function)

퍼셉트론에서는 `activation function`이라는 활성화 함수가 존재한다. 이는 입력신호의 총합을 출력신호로 변환하는 함수를 뜻한다. activation function이 왜 필요하냐 하면, 우선 결론부터 말하자면 비선형분리를 하기 위해서이다. 

이전 단층 퍼셉트론에서는 단순하게 가중치와 입력신호 편향의 합으로 식이 구성되었다. 

그런데 다층퍼셉트론에서도 활성화함수가 없다면(혹은 활성화 함수가 선형함수라면) 이전 값이 다음층으로 넘어와 다시 가중치를 곱해주는 것은 맞지만 역시나 선형식 형태로 구성이 된다 

 다시 요약하자면 위의 식에서 볼 수 있듯이 $ W_2 $가 곱해졌음에도 결국 식을 전개하고 일반화하면 단순 선형식이 되어버린다. 이는 역시 퍼셉트론의 한계와 동일하고, 이를 해결하기 위해 선형을 비선형으로 바꿔주기 위하여 비선형 활성화 함수를 사용하게 된다. 또한 퍼셉트론에서 사용되던 계단함수는 미분이 불가능한 지점이 있고 미분으로 해도 0이 나오기 때문에 역전파와 같은 기법을 사용할 수 없다. 

https://hwk0702.github.io/ml/dl/deep%20learning/2020/07/09/activation_function/

위와 같이 다양한 활성화 함수들이 있으며 기존의 단층 퍼셉트론은 아래와 같은 `계단함수(Step function)` 을 이용하여 1 혹은 0의 출력을 냈었다. 

https://commons.wikimedia.org/wiki/File:Step_function.svg

활성화 함수들은 단순 0, 1이 아니라 다양한 실수값들을 내게 되며 미분가능한 함수이다.

이러한 미분가능성은 모델 학습과정에서 중요하게 다뤄지게 된다. 

위에서 나타난 다양한 활성화함수에 대한 설명은 이후 모델 학습에 대하여 배운 다음 따로 작성해 보도록 하겠다.