이번에는 역전파 알고리즘에 대하여 알아볼 것이다.
0. 역전파 배경
이전에 확률적, 미니배치 경사하강법이 등장한 이유를 Loss 값을 계산을 할 때 모든 데이터 셋에 대하여 계산하는 것이 아니라, 학습 샘플(1 혹은 배치사이즈)만큼의 평균 Loss값을 이용하여 계산을 효율적으로 하였다.
그러나 경사하강법을 진행하기 위해서는 모델을 구성하는 각 파라미터에 대한 손실함수를 미분한 결과(그래디언트)는 여전히 계산해야 한다. 이 모든 파라미터에 대한 미분값을 그래디언트 하고 불렀다.
이때, 모든 파라미터에 대한 편미분을 효율적으로 하기 위해 역전파란 개념이 등장하였다.
손실함수가 단순 선형식일 경우 각 파라미터에 대하여 편미분 하는 것은 간단하다.
예를 들어, 모델을 $ y=ax+b $라하고, 손실함수로 MSE를 사용한다고 해보자. 그럼 손실함수의 값은 다음과 같다.
$$ L_{\text{MSE}} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2= \frac{1}{n} \sum_{i=1}^{n} (y_i - (ax_i + b))^2$$
이럴 경우, 파라미터(a, b)를 업데이트하기 위해 그래디언트를 계산하려면 a와 b에 대하여 이 손실함수 식을 미분해야 한다. a에 대하여 편미분을 하면 $ \frac{\partial L_{\text{MSE}}}{\partial a} = -\frac{2}{n} \sum_{i=1}^{n} x_i (y_i - (ax_i + b)) $가 되고, b에 대하여 편미분을 하면 $ \frac{\partial L_{\text{MSE}}}{\partial b} = -\frac{2}{n} \sum_{i=1}^{n} (y_i - (ax_i + b)) $ 이다. 이제 이러한 각각의 손실함수에 대한 편미분값에 lr을 곱해서 파라미터를 업데이트해주면 된다.
그러나 모델이 복잡해진다면 이러한 편미분을 계산하는 것은 매우 어려운 과정이다. 우 `계산 그래프`를 잠깐 설명해 보겠다
1. 계산 그래프
계산 그래프란 일련의 연산과정을 하나의 방향 그래프로 나타내는 것을 말하며, `노드`와 `엣지`로 구성된다.
노드(node)는 하나의 연산을 의미하고, 엣지는 노드에 필요한 입력값들을 의미한다.

계산 그래프는 전체 편미분에 필요한 연산들을 잘게 쪼개서 계산한 다음 합치는 과정을 통해 최종 결과를 도출하는데 도움을 주기 위하여 사용한다.
계산 그래프에 대하여 간단한 예시를 들어보자.

2. 순전파
위의 그림과 같이 100원짜리 사과 2개 / 150원짜리 귤 3개를 사는데 소비세가 1.1% 붙는다고 해보자.
1. 사과를 중심으로 볼 때, 100원과 2개는 각각 입력값(엣지)를 의미한다. 이 둘의 연산(노드)을 통해(여기서는 구매하는 거니까 곱연산) 200이 다음 엣지로 넘어간다.
2. 귤을 중심으로 볼 때 , 150 원고 3개의 연산을 통해 450이 다음 엣지로 넘어간다.
3. 굴과 사과를 중심으로 200과 450의 연산을 통해 650이 다음 엣지로 간다.
4. 소비세 1.1이 엣지로 들어온다.
5. 소비세와 사과와 귤을 구매가격의 합 1.1과 650의 연산을 통해 715가 최종 결과로 도축된다.
귤, 사과, 소비세들을 각각의 파라미터(가중치와 편향)로 볼 때 이러한 단순 계산과정을 `순전파(forward propagation)`라고 한다.
3. 연쇄법칙
이제 역전파의 핵심인 `연쇄법칙(chain rule)`을 알아볼 것이다. 연쇄법칙이란, 둘 이상의 연산이 수행된 `합성함수`를 미분하는 방법이다. 합성함수 $ f(g(x)) $ 를 미분하면 다음과 같이 연쇄법칙을 통해 나타낼 수 있다.
$$ \frac{df(g(x))}{dx} = \frac{df(g(x))}{dg(x)} \cdot \frac{dg(x)}{dx} $$
즉 바로 $f(g(x))$를 $x$에 대하여 미분하는 것이 아니라, 중간결과를 도입하여 $g(x)$에 대하여 미분하고 또 $g(x)$를 $x$에 대하여 미분하자는 것이다. 이렇게 되면 한 번에 미분하는 것보다 덜 복잡한 식들을 미분하는 과정이다.
실제 식을 통해서 확인해 보자.
$ z=(x+y)^2 $라 할 때 이식을 미분해 볼 것이다. 계산의 편의상 $(x+y)=w$로 치환하겠다.
우선 chain rule에 따르면 $$ \frac{\partial z}{\partial x} = \frac{\partial z}{\partial w} \frac{\partial w}{\partial x} $$로 나타낼 수 있다. 이렇게 되면$\frac{\partial z}{\partial w}$를 계산해야 하는데 $z=(x+y)^2=w^2$ 이므로, $ \frac{\partial z}{\partial w}=2w $가 되고, $ \frac{\partial w}{\partial x}=1$ 이된다. 따라서 $ \frac{\partial z}{\partial x} = 2w \cdot 1 = 2w $가 된다.
이렇게
4. 역전파
이 연쇄법칙을 계산하는 방식을 기억해 두고 이제 역전파에 대하여 알아볼 것이다.

위와 같이 4개의 노드로 구성된 neural net을 생각해 보면 파라미터가 p1, p2, p3, p4로 구성되어 있다.
우선 각 샘플에 대하여 파라미터를 적용하여 손실함수의 값을 구하는 것을 순전파였다.
이후 각 파라미터 업데이트를 하기 위하여 경사하강법을 적용해야 하는데, 손실함수에 대한 각 파라미터 p1, p2, p3, p4의 미분값이 있어야 한다. 즉 우리는 $ \frac{\partial L}{\partial p_1}, \frac{\partial L}{\partial p_2}, \frac{\partial L}{\partial p_3}, \frac{\partial L}{\partial p_4} $ 을 구해야 한다.
이때 $ \frac{\partial L}{\partial p_4} $ 는 구하기 쉽다 그냥 L에 대하여 미분을 바로 진행하면 된다.
다음으로 $ \frac{\partial L}{\partial p_3} $ 을 계산해야 하는데, 이 과정에서 연쇄법칙을 사용하면 더 빠르고 효율적으로 계산할 수 있다. 바로 중간과정을 도입하는 건데, 연쇄법칙을 적용하면 $ \frac{\partial L}{\partial p_3} = \frac{\partial L}{\partial p_4} \cdot \frac{\partial p_4}{\partial p_3} $ 가 된다. 이때 이미 $\frac{\partial L}{\partial p_4} $는 이전 파라미터 p4를 계산할 때 구해놨다. 이 방식으로 p2를 업데이트할 때는 p3를 계산할 때 구한 값에다가 p3를 p2로 미분한 것만 곱해주면 된다. 이런식으로 반복하는 것이다. 이렇게 순전파와 반대방향으로 L에서부터 오는 과정을 `역전파`라고 부른다.
한마디로 역전파는 신경망의 추론 방향과 반대되는 방향으로 순차적으로 오차에 의한 편미분을 수행하여 각 레이어의 파라미터를 업데이트하는 과정을 의미한다.

즉, 각 노드에 대한 편미분을 (이전편미분) 기존신호에 곱하여 이전레이어의 노드로 전달한다.
대표적인 역전파에 대하여 알아보자. 우선 대부분의 노드(연산)는 곱셈과 덧셈으로 이루져있다.
4-1. 덧셈노드 역전
이해를 돕기 위해 또 예시를 들어보자.
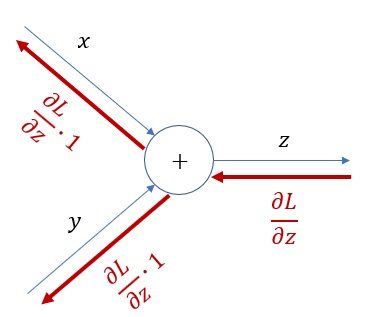
출력이 $z=x+y$ 를 의미하고, 각 파라미터 x와 y에 대해 역전파를 계산해 보면 우선 $ \frac{\partial L}{\partial x} = \frac{\partial L}{\partial z} \cdot \frac{\partial z}{\partial x} $이고, $z= x + y $ 이므로, $ \frac{\partial z}{\partial x} $는 1이다.
반대로 $\frac{\partial L}{\partial y} = \frac{\partial L}{\partial z} \cdot \frac{\partial z}{\partial y} $이고,$ \frac{\partial z}{\partial y} $도 1 이다. 즉, 덧셈노드일 경우 이전까지 계산된 그래디언트( $ \frac{\partial L}{\partial z} $)이 그대로 넘어가게 된다.
4-2. 곱셈노드
다음으로 곱셈노드를 보자. 식은 동일하다. 우선 $ \frac{\partial L}{\partial x} = \frac{\partial L}{\partial z} \cdot \frac{\partial z}{\partial x} $이고, $ z= x \cdot y $ 이므로, $ \frac{\partial z}{\partial x} $는 $y$가 된다.
마찬가지로 $y$에 대하여 진행해 보면 $ \frac{\partial L}{\partial y} = \frac{\partial L}{\partial z} \cdot \frac{\partial z}{\partial y} $이고,$ z= x \cdot y $ 이므로, $ \frac{\partial z}{\partial y} $는 $x$ 이다.
즉 곱셈노드의 경우, 이전까지 계산된 그래디언트에 반대편 엣지의 값을 곱하게 된다.

이 위의 2가지를 기억하면 쉽게 계산할 수 있을 것이다.
4-3. 역전파 계산
자 이제 실제 에시를 들어서 설명해 보자. 아래와 같이 함수, 입력 데이터, 타겟값이 있다고 해보자.
이 값들을 이용하여 파라미터 업데이트 하는 과정을 살펴보자.
$$ \text{함수:} f(x,y,z) = (x+y)z $$ $$ \text{데이터:} x=-2, y=5, z= -4, target = -10 $$ $$ \text{손실함수:} L= MSE = (target-f)^2 $$
이를 계산 그래프로 표현해 보면 다음과 같다.

1. 순전파 진행.
우선 입력값에 대한 계산을 순방향으로 진행하면 예측값은 -12가 나온다.
2. 역전파 진행
파라미터 업데이트를 위해 경사하강법을 사용하려면 각 파라미터에 대한 미분값 즉 손실함수의 그래디언트를 알아야 한다.
자 우리가 구해야 하는 값들은 아래의 좌변에 해당하며, 그 값들을 연쇄법칙을 이용하면 우변처럼 풀어낼 수 있다.
$$ \frac{\partial L}{\partial f} = \frac{\partial L}{\partial f} \cdot \frac{\partial f}{\partial f} $$
$$ \frac{\partial L}{\partial x} = \frac{\partial L}{\partial f} \cdot\frac{\partial f}{\partial x} $$
$$ \frac{\partial L}{\partial y} = \frac{\partial L}{\partial f} \cdot\frac{\partial f}{\partial y} $$
$$ \frac{\partial L}{\partial z} = \frac{\partial L}{\partial f} \cdot\frac{\partial f}{\partial z} $$
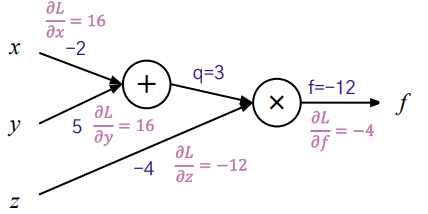
우선 공통되는 값 $ \frac{\partial L}{\partial f} = 2(f-target) = 2(-12-(-10)) = -4 $ 가 된다.
다음으로 뒤에서부터 계산하기 때문에 $ \frac{\partial L}{\partial z} $를 보면, $ \frac{\partial f}{\partial z} $ 이 값을 알아야 한다. 위에서 배운 곱노드의 역전파에 따르면 곱연산의 경우, 이전 그래디언트 값에 반대편 엣지의 값을 곱한다.
따라서 $ \frac{\partial f}{\partial z}= \frac{\partial f}{\partial f} \cdot 3 $ 이 된다. 이때 이 3은 반대편 엣지인 (x+y) 즉 q를 나타낸다. 다음으로 q에 대한 그래디언트는$ \frac{\partial f}{\partial q} = \frac{\partial f}{\partial f} \cdot -4 $ 이때 -4는 반대편 엣지의 값 z=-4를 의미한다.
다음으로 덧셈노드의 역전파에 따라, x와 y 각각의 그래디언트는 이전 그래디언트를 그대로 가져오게 된다. 즉 q의 그래디언트를 그대로 가져오게 된다.
그럼 최종적으로 위의 값들을 확인해 보면, 아래와 같다.
$$ \frac{\partial L}{\partial f} = \frac{\partial L}{\partial f} \cdot \frac{\partial f}{\partial f} = -4 \cdot 1 = -4$$
$$ \frac{\partial L}{\partial x} = \frac{\partial L}{\partial f} \cdot\frac{\partial f}{\partial x} = -4 \cdot -4 = 16 $$
$$ \frac{\partial L}{\partial y} = \frac{\partial L}{\partial f} \cdot\frac{\partial f}{\partial y} = -4 \cdot -4 = 16$$
$$ \frac{\partial L}{\partial z} = \frac{\partial L}{\partial f} \cdot\frac{\partial f}{\partial z} = -4 \cdot 3 = -12 $$

이렇게 각 파라미터에 대한 편미분 값을 구했기 때문에 경사하강법에 의거하여,
$ x \leftarrow x-lr \cdot \frac{\partial L}{\partial x} $, $ y\leftarrow y-lr \cdot\frac{\partial L}{\partial y} $, $ z\leftarrow z-lr \cdot\frac{\partial L}{\partial z} $이므로,각각을 계산하여 파라미터를 업데이트해준다.

'ML & DL > 개념정리' 카테고리의 다른 글
| PyTorch 시작 (0) | 2023.12.21 |
|---|---|
| 손실 함수(Loss function) (1) | 2023.12.21 |
| Gradient Descent: 경사하강법 (1) | 2023.12.20 |
| 퍼셉트론과 다층 퍼셉트론(MLP) (0) | 2023.12.19 |
| 딥러닝 개요 (0) | 2023.12.19 |
