텐서란 데이터의 배열(array)을 의미한다.

1. 텐서의 연산
1-1. 사칙연산
텐서의 사칙연산은 단순하게 원소 단위로 연산하는 것을 의미한다.
다음과 같이 같은 행, 열에 있는 원소들끼리 사칙연산을 수행하면 된다.

1-1-1. 사칙연산 코드
tensor_a = torch.tensor([[1, -1], [2, 3]])
tensor_b = torch.tensor([[2, -2] ,[3, 1]])
print('덧셈')
print("a+b : \n", tensor_a + tensor_b)
print("torch.add(a,b) : \n", torch.add(tensor_a, tensor_b))
print('뺄셈')
print("a-b : \n", tensor_a - tensor_b)
print("torch.sub(a,b) : \n", torch.sub(tensor_a, tensor_b))
print('곱셈')
print("a*b : \n", tensor_a * tensor_b)
print("torch.mul(a,b) : \n", torch.mul(tensor_a, tensor_b))
print('나눗셈')
print("a/b : \n", tensor_a / tensor_b)
print("torch.div(a,b) : \n", torch.div(tensor_a, tensor_b))1-2. 내적(Inner Product)
내적은 1D 텐서 단위에서만 가능하다.

1-2-1. 내적 코드
v1 = torch.tensor([1, 2])
u1 = torch.tensor([3, 4])
print("v1.dot(u1) : ", v1.dot(u1)) # v1 과 u1 내적 (torch.tensor 에도 dot 함수 존재)
print("torch.dot(v1, u1) : ", torch.dot(v1, u1)) # v1 과 u1 내적1-3. 행렬 곱 연산
두 행렬의 대응하는 행과 열의 원소들을 곱한 뒤 더하는 방식 = 행과 열 단위로 내적
이 떄, 앞의 행렬의 열과 뒤의 행렬의 행의 길이가 같아야 한다.

1-3-1. 행렬 곱 코드
A = torch.tensor([[1, 2], [3, 4]]) # (2,2) Tensor
B = torch.tensor([[-1, 2], [1, 0]]) # (2,2) Tensor
print("A: ", A)
print("B: ", B)
print("AB : ", torch.matmul(A, B)) # A에서 B를 행렬곱
print("BA : ", B.matmul(A)) # B에서 A를 행렬곱1-4. Broadcasting
차원이 다른 두 텐서 혹은 텐서와 스칼라 간 연산을 가능하게 해주는 기능.

1-4-1. Broadcasting 코드
! 차원이 다를 때 무조건 계산되는 것은 아님.
tensor_a = torch.randn(3, 2)
print("Original : \n", tensor_a)
## 0 행의 모든 열을 10 으로 변경하기
tensor_a[0, :] = 10 # 0행의 모든 열에 broadcasting 을 통한 scalar 값 대입
print("변경된 텐서 : \n", tensor_a)
tensor_a = torch.randn(3, 2)
print("Original : \n", tensor_a)
## 모든 값을 tensor [0,1]로 변경하기
tensor_a[:, :] = torch.tensor([0, 1]) # 모든 값에 접근하여 [0,1] 로 변경
print("변경된 Tensor : \n", tensor_a)2. Dense Tensor, Sparse Tensor
`Dense Tensor`은 배열의 모든 위치에 값을 가지는 텐서를 의미.
`Sparse Tensor`은 0이 아닌 원소와 그 위치를 저장하는 텐서.
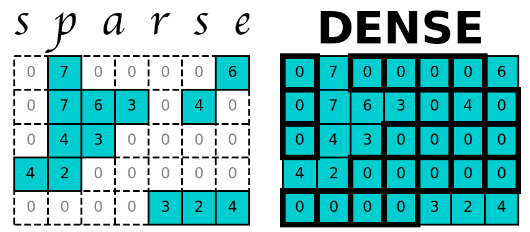
Dense Tensor은 생략가능한 원소까지 모두 저장하기 때문에 Tensor의 크기와 비례하게 메모리를 사용하게 되어 Out of memory 문제가 발생할 수도 있으며, 많은 계산양으로 인하여 계산시간이 증가한다.
이를 위해 Tensor에 0이 많을 경우에, 효율적인 메모리 사용을 위해 Spare Tensor이 등장하였고 이는 계산시간이 감소된다는 장점이 존재한다. 이 Sparse tensor을 구현하는 방식은 여러 가지가 있는데 COO방식, CSR방식, CSC방식 만 알아보겠다. 더 많은 방법은 다른 곳을 참고해 보면 좋을 것 같다.
Sparse Matrices · Matt Eding
Sparse Matrices 25 Apr 2019 Data Structures - Sparse Matrices Table of Contents Introduction Construction Matrices Coordinate Matrix Linked List Matrix Dictionary of Keys Matrix Compressed Sparse Matrices Compressed Sparse Row/Column Block Sparse Row Diago
matteding.github.io
2-1. Sparse COO Tensor
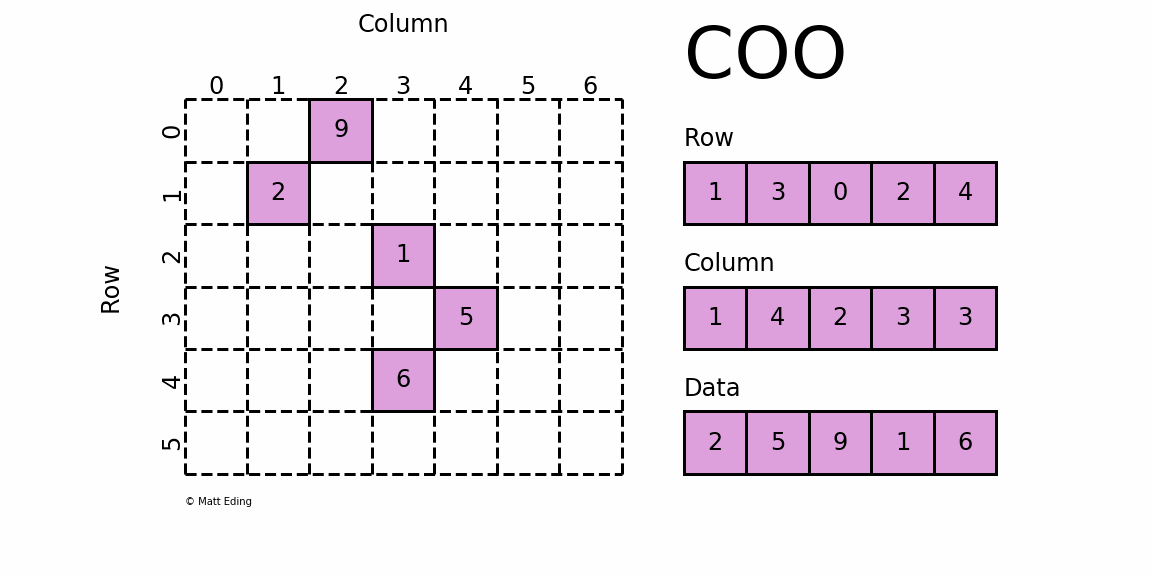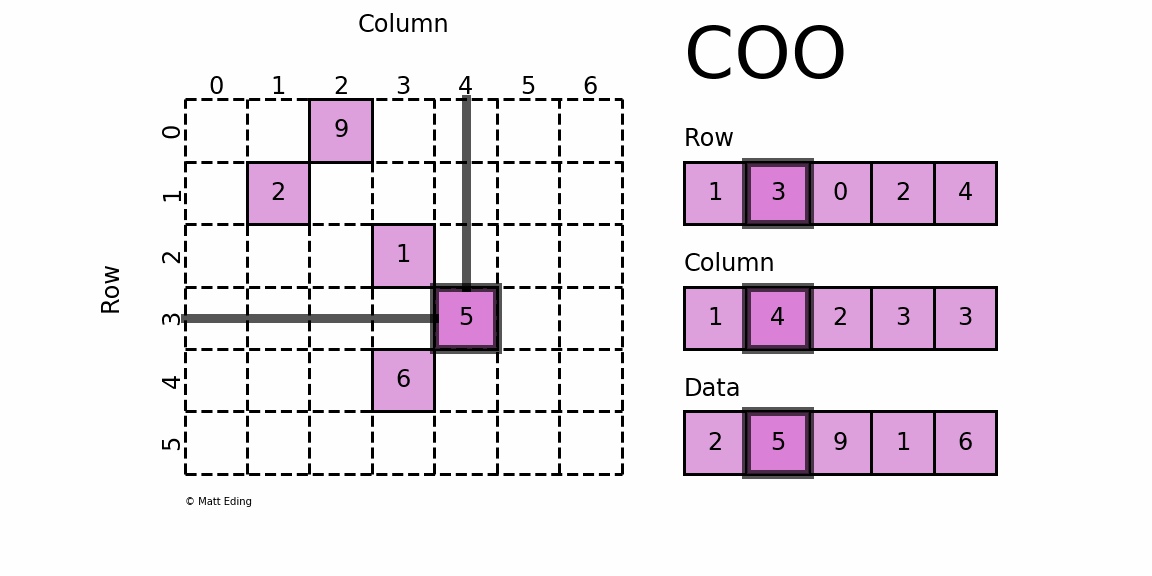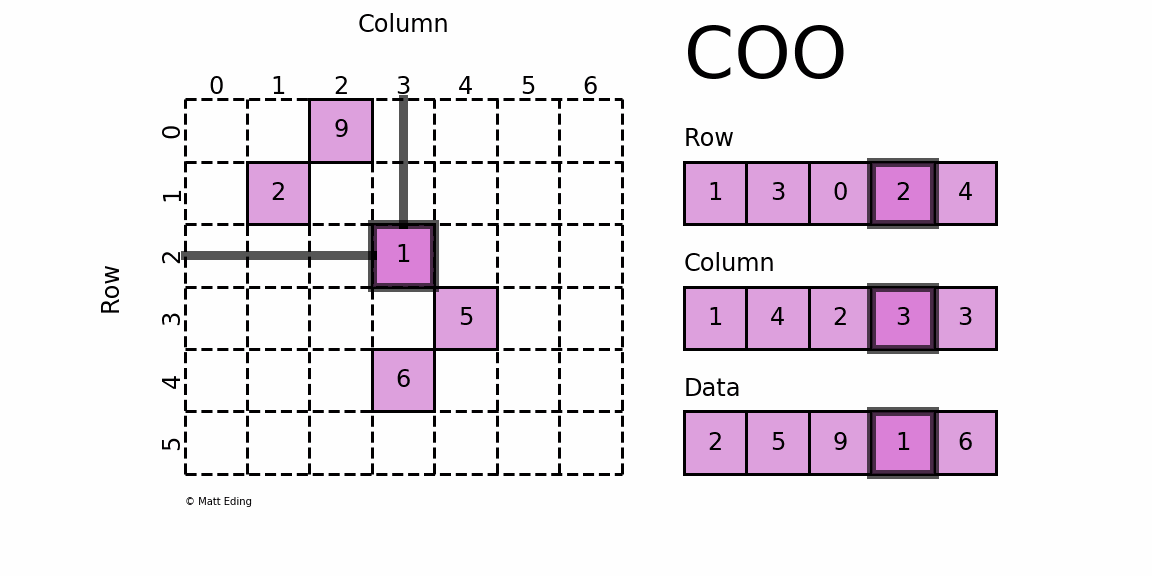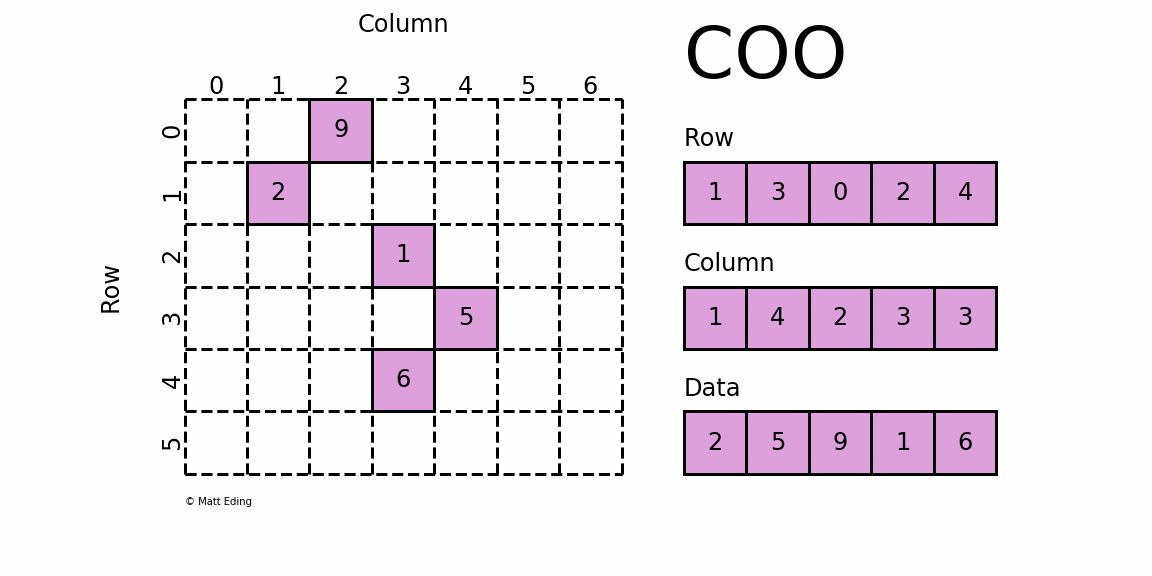
(row_idx,col_idx,value)의 형태로 저장하는 방식. idx는 0이 아닌 값의 위치로 나타내는 방식.
이 방식은 직관적이지만, 원소가 위치한 행과 열 인덱스를 별도로 저장하고 있기 때문에 반복해서 저장되는 값이 발생하여 비효율적인 메모리를 사용하게 되고, 원소에 접근할 때마다 행-열 인덱스와 값을 찾아야 해서 연산 성능이 저하된다.
2-1-1. Sparse COO Tensor 코드
# dense tensor -> sparse coo tensor
a = torch.tensor([[0, 2.], [3, 0]])
a.to_sparse()
# 바로 sparse tensor 생성
indices = torch.tensor([[0, 1, 1],[2, 0, 1]]) # 0이 아닌 값의 (index, column) pairs
values = torch.tensor([4, 5, 6]) # 0 이 아닌 값의 values, values의 사이
sparse_tensor = torch.sparse_coo_tensor(indices = indices, values = values, size=(2, 3)) # (2,3)의 sparse tensor
print(sparse_tensor)
print(sparse_tensor.to_dense())2-2. Sparse CSR Tensor
(row_pointer,col_idx,value)의 형태로 저장하는 방식. pointer=경계를 표시하는 배열
이 방식은 원소를 순회하는 방식으로 접근 가능하여 효율적이고, 중복 저장이 줄어들어 효율적인 메모리사용이 가능하다. 그러나 구조가 복잡하여 직관적이지 않다.
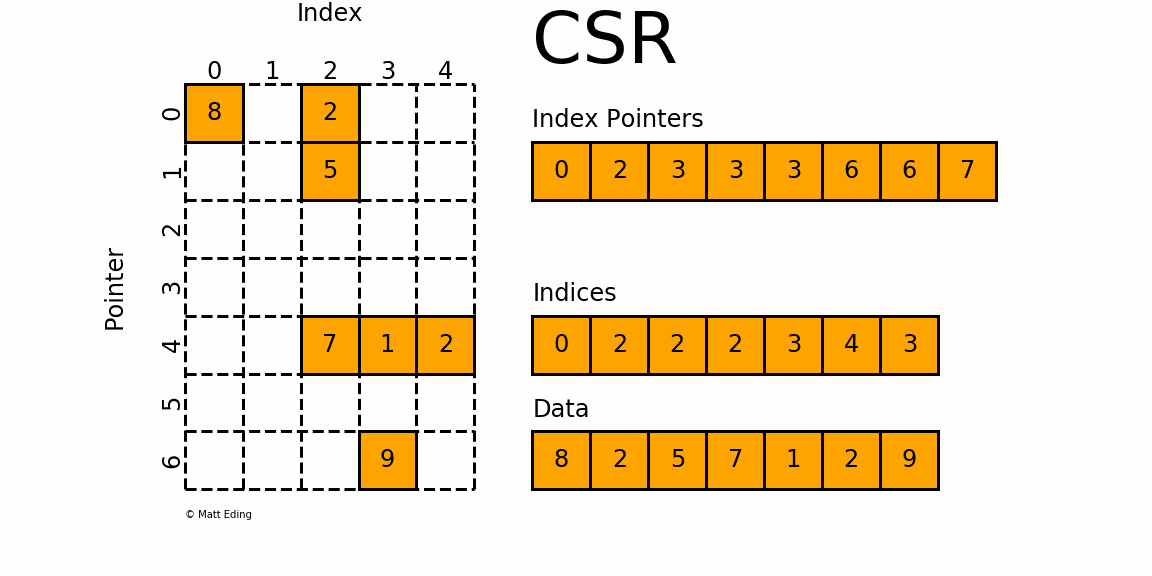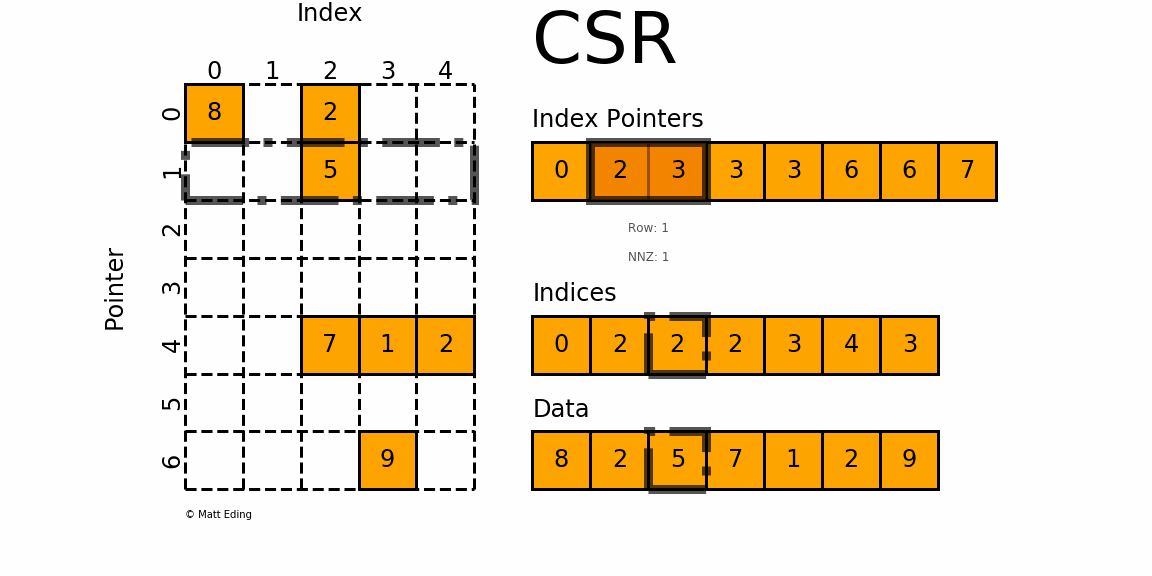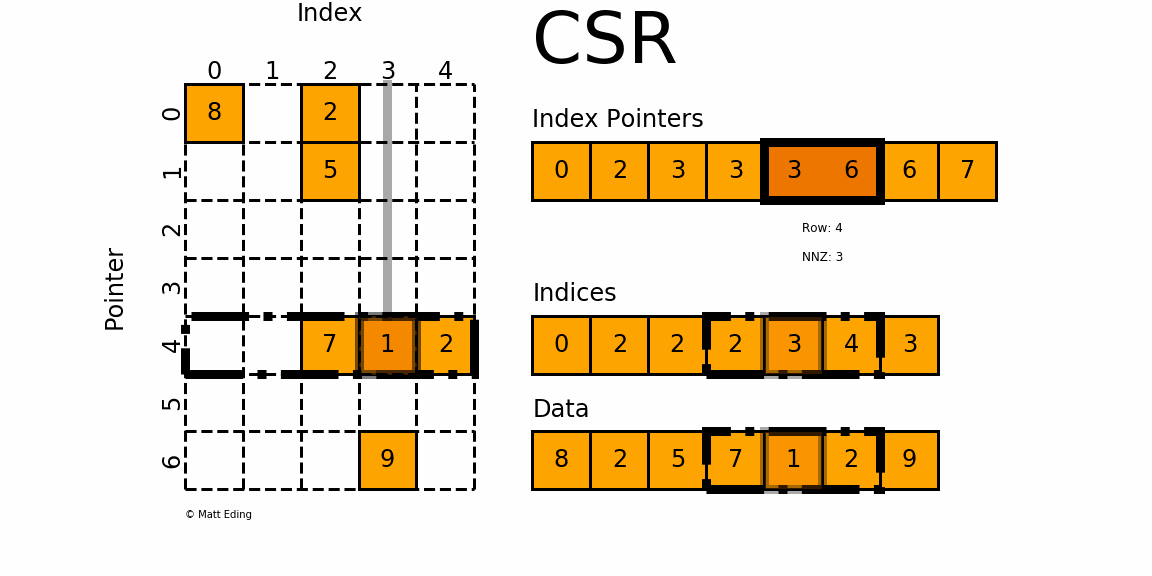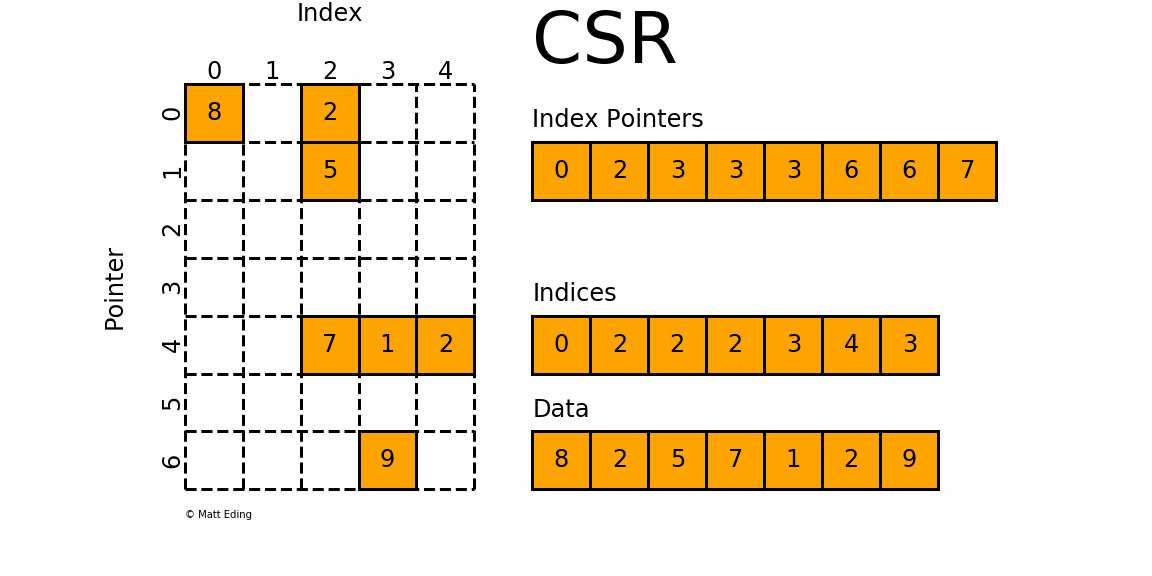
2-2-1. Sparse CSC Tensor 코드
# dense tensor -> sparse csr tensor
t = torch.tensor([[0, 0, 4, 3], [5, 6, 0, 0]])
print(t)
t.to_sparse_csr()
# 바로 spase csr tensor 생성
crow_indices = torch.tensor([0, 2, 2]) # 0이 아닌 행의 위치 (첫번쨰는 무조건 0), 즉 row_pointer
col_indices = torch.tensor([0, 1]) # 0이 아닌 열의 위치
values = torch.tensor([1, 2]) # 0이 아닌 값
csr = torch.sparse_csr_tensor(crow_indices = crow_indices, col_indices = col_indices, values = values)
print(csr)
print(csr.to_dense())2-3. Sparse CSC Tensor
(col_pointer,row_idx,value)의 형태로 저장하는 방식.
위의 CSR과 동일한 장단점을 가지고 있다.

2-3-1. Sparse CSC Tensor 코드
# dense tensor -> sparse csc tensor
t = torch.tensor([[0, 0, 4, 3], [5, 6, 0, 0]])
print(t)
t.to_sparse_csc() # Dense Tensor 를 CSC Spare tensor 형식으로 변환
# 바로 sparse csc tensor 생성
ccol_indices = torch.tensor([0, 2, 2]) # 0이 아닌 열의 위치 (첫번쨰는 무조건 0), 즉 column_pointer
row_indices = torch.tensor([0, 1]) # 0이 아닌 행의 위치
values = torch.tensor([1, 2]) # 0이 아닌 값
csc = torch.sparse_csc_tensor(ccol_indices = ccol_indices, row_indices = row_indices, values = values)
print(csc)
print(csc.to_dense())2-4. Sparse Tensor 조작
현재까지 Sparse Tensor에서 사칙연산은 3차원까지 가능하고, 행렬곱은 2차원까지만 가능하다. 또한 CSR과 CSC의 3차원 Tensor은 곱셈도 불가능하다.
Sparse Tensor도 인덱싱은 가능하나, 슬라이싱은 불가능하다.
torch.sparse — PyTorch 2.1 documentation
Shortcuts
pytorch.org
'ML & DL > 개념정리' 카테고리의 다른 글
| Linear, Lasso, Ridge Regression (0) | 2023.12.27 |
|---|---|
| Random Forest: 랜덤포레스트 (0) | 2023.12.26 |
| Data Augmentataion: 데이터 증강 (0) | 2023.12.26 |
| 최적화 알고리즘 (0) | 2023.12.26 |
| 가중치 초기화, 규제, 학습 (0) | 2023.12.26 |
