Linear Regression 은 $y=Wx+b$로 표시되는 선형식으로 $x$와 $y$사이의 관계를 찾는 모델이다.
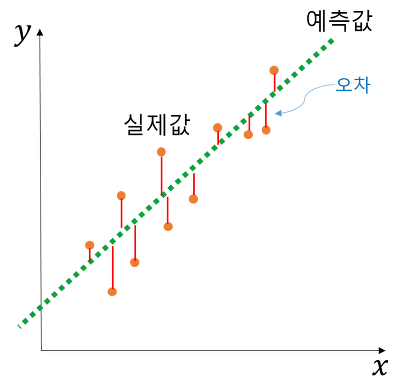
분류와는 다르게 회귀 모델은 선형식의 계산결과 자체가 예측값이다.
이 선형회귀의 관계식을 찾을 때 실제 현실에서는 오차가 0일 수없기 때문에 선형회귀란, 오차가 가장 적게 되는, 즉 관계를 가장 잘 대변하는 식을 찾는 것이라고 할 수 있다.
따라서 오차가 가장 적게 되도록 학습을 진행하며 가장 많이 사용되는 Loss function은 `MSE:Mean Squared Error`이다.
각 loss function에 대한 설명은 아래에 자세하게 설명하였다.
간단하게만 말하자면, MSE는 outlier 데이터가 있다면 오차가 매우 크게 나오기 때문에 미리 이상치등을 제거해줘야 한다.
Evaluation metric(평가지표)
모델 성능 평가란, 실제값과 모델에 의해 예측된 값의 차이를 구하는것. 실제값과 예측값이 오차가 0인 것은 실질적으로 힘들기 때문에 오차의 한계를 정해서 그 오차까지는 허용해준다. 성능평
changsroad.tistory.com
이렇게 오차를 줄이는 방법으로 학습을 하며, 파라미터 $W$와 $b$를 찾는 문제이다.
이 파라미터들을 찾기 위해서는 다양한 방법이 있는데 가장 대표적인 것이 OLS와 경사하강법이 있다. 대표적인 선형회귀를 구현한 파이썬의 scikit-learn에서는 이 OLS: Ordinary least squared, 최소자승법(최소제곱법)을 이용하여 구현되었다.
OLS에 대한 설명은 다른 작성자님의 글로 대체하겠다.
최소 제곱법 (Least Square Method = OLS)
최소제곱법이란, "Least Square Method" or "Ordinary Least Square"으로 불리며 오차를 최소화 시키는 방법으로 회귀 계수($\beta_0, \beta_1$)를 추정하는 기법입니다. 단순 선형 회귀(이하 회귀)란 설명변수와 반
laoonlee.tistory.com
이 선형회귀는 통계적으로 설명 가능한 이론이 많고, 선형식의 형태로 설명이 가능하다. 또한 모델이 간단하기 때문에 복잡한 모델들보다 성능이 우수할 때도 있어 자주 쓰이는 모델이다.
또한 식에서 독립변수 X가 한 개인 경우를 `단순 선형회귀분석`이라고 부르며, 독립변수 X가 여러 개일 때를 `다중 선형회귀분석`이라고 부른다.
2. Lasso
Lasso는 Linear Regression 모델이 고차원 공간에 overfitting이 쉽게 되는 문제를 해결한 기법이다.
기존 선형회귀의 식이 $y=Wx+b$였다면, Lasso는 가중치의 L1 규제를 Loss function에 더해준다. 따라서 Loss가 무조건 증가하게 된다. 이 L1규제를 제약조건이라고 부른다.
이제 Loss가 최소가 되기 위해서는 앞부분의 MSE가 최소가 되게하는 가중치와 편향을 찾으면서, 뒷부분의 가중치들의 절대값의 합이 최소가 되게 해야만한다. 이 말은 뒤쪽 부분이 0에 가깝게 되야한다는 것이며 이를 위해서는 특정 특징들은 모델을 만들때 사용되지 않게 만든다. 즉 요약하면, Lasso는 덜 중요한 특성의 가중치를 제거하기 위함이다.
아래 그림에서 mse가 최소가되는 빨간원과 w의 절대값의 합을 나타내는 마름모가 만날 때가 최소인 값이다.
즉 마름모의 꼭지점에 닿는 그 지점은 어떤 특정 $\beta$값들이 0인 지점을 위치한다.
$$ \sum_{i=1}^{n} (y_i - w^Tx_i)^2 + \lambda \sum_{j=1}^p |w_j|$$

3. Ridge
Ridge도 linear Regression 모델이 고차원 공간에 overfitting되는 문제를 보완하기위해 등장하였으며, L2규제를 추가하여
나타낸다. $$ \sum_{i=1}^{n} (y_i - w^Tx_i)^2 + \lambda \sum_{j=1}^p w_j^2 $$
Ridge의 중요한점은 페널티항의 계수를 0에 근사하도록 축소하나 0이될순없다. 따라서 변수가 줄어들지는 않는다

정리하자면 Lasso나 Ridge를 적용했을 때, 성능이 향상되었다면 모델에 사용하는 feature vector가 차원을 줄일 필요가 있다는 것, 즉 feature selection이 필요하다는 것이다.
또한 위에서 말했듯 Ridge의 가중치들은 0에 가까워질뿐 0이 되지는 않기 떄문에 모든 변수의 영향을 계산한다.
따라서 특성의 중요도가 전체적으로 비슷하다면 릿지, 특성들끼리 편차가 크다면 라쏘가 더 적합한 학습을 한다.
'ML & DL > 개념정리' 카테고리의 다른 글
| PyTorch-DNN, CNN을 이용한 MNIST 실습 (0) | 2024.01.02 |
|---|---|
| 딥러닝 발전 (0) | 2023.12.28 |
| Random Forest: 랜덤포레스트 (0) | 2023.12.26 |
| PyTorch- 텐서 조작 (0) | 2023.12.26 |
| Data Augmentataion: 데이터 증강 (0) | 2023.12.26 |