이번시간에는 데이터 전처리 과정에 포함되어 있는 연속형 변수와 범주형 변수를 처리하는 과정에 대하여 알아볼 것이다.
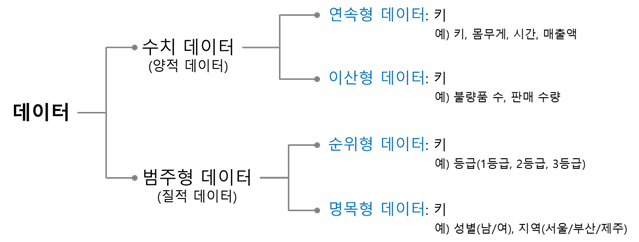
우선 데이터, 변수는 위와 같이 크게는 수치형과 범주형으로 나뉘고 각각 연속형과 이산형 그리고 순위형과 명목형으로 분류된다. 모델에 input 데이터를 넣기전에 연속형이나 범주형 변수의 처리를 진행해줘야 제대로 모델이 돌아가며 성능이 좋아질 수 있다.
각각의 변수는 다음과 같은 처리를 진행할 것이다.
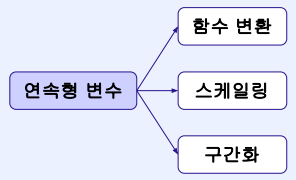

1. 연속형 변수
1-1. 함수변환
1-1-1. Log Transform
로그변환이란 비대칭된 임의의 분포를 정규분포에 가깝게 전환시키는 역할을 한다. 데이터를 정규화시키는 것은 모델의 성능을 향상시키는데 도움을 주며, 로그화를 통해서 데이터의 스케일을 작게 만들어 데이터 간의 편차를 줄이는데 도움을 준다. 예를 들어 데이터가 `10`,`100`,`1000` 이었던 것을 로그변환을 하면 `1`,`2`,`3`으로 줄어든다
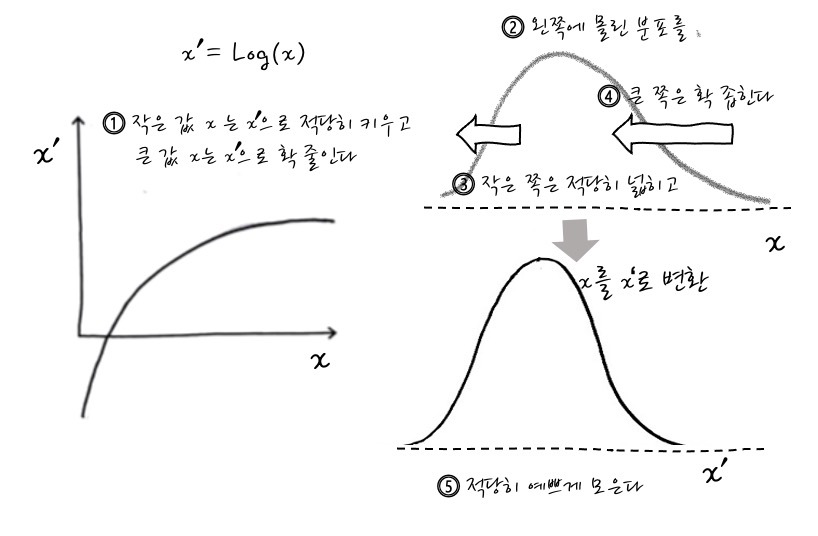
로그변환을 통해서 비대칭 분포를 제거할 수 있고 이상치 완화에 효과적이지만 0이나 음수를 처리할 수 없다.
1-1-2. Square Root Transform
제곱근 변환이란 말 그대로 변수에 제곱근을 적용하는 것을 말한다. 앞의 로그변환가 유사하게 정규성, 선형관계 생성, 데이터 스케일 축소, 이상치 완화 등의 특징이 있다.
로그변환과의 차이점은 변환시 데이터를 줄여주는 강도가 다른데, 비대칭이 심할경우에는 로그변환을, 비대칭이 약한 경우에는 제곱근 변환을 주로 사용한다.
위의 두 변환은 모두 큰값은 더 작게 바꾸는 성질을 가지고 있기 때문에 만약 오른쪽으로 치우져진 그래프에 적용할 경우 오히려 비대칭성이 강해지게 될 수 있으니 반드시 데이터의 분포를 보고 변환을 진행해야한다.
1-1-3. Power Transform
거듭제곱 변환도 변수에 거듭제곱을 적용하여 변환하는 것을 말하며, 작은 값을 크게, 큰값은 더 크게 바꿔주는 역할을 한다.
1-1-4. Box-Cox Transfrom
$$ f(x;\lambda) = \begin{cases} \frac{{x^\lambda - 1}}{{\lambda}}, & \text{if } \lambda \neq 0 \\ \log(x), & \text{if } \lambda = 0 \end{cases} $$
Box-Cox 변환은 $\lambda$에 따라 다양한 변환을 하는 방법으로 목적에 맞게 적절한 $\lambda$를 찾아야한다. $\lambda$에 따른 변환은 아래와 같다.

1-2. Scaling
스케일링이란 변수를 동일한 범위로 변경하는 것을 말한다. 예를 들어 몸무게라는 변수와 키라는변수가 있을 때 키는 보통 100이상의 단위들이고 몸무게는 70이하의 단위들이다.
일반적으로 독립 변수들의 수치범위가 다르게 존재하면 종속 변수에 다른 영향을 미치며, 수치 범위가 클 수록 다른 변수에 비해 중요하게 작용될 수도 있다.따라서 스케일을 동일하게 만들어줌으로써 이러한 영향을 제외시키려는 것이다.
특히 거리기반의 알고리즘(KNN)에서 변수들이 다른 스케일을 가지고있으면 결과가 올바르지 않게 나올 수 있다.

1-2-1. Min-Max 스케일링

$$ X_{\text{scaled}} = \frac{X - X_{\text{min}}}{X_{\text{max}} - X_{\text{min}}} $$
연속형 변수의 수치 범위를 0~1사이로 변환하는 방법.
그러나 모든 수위범위가 같아지기 때문에 이상치에 취약하다. 만약 아주 큰 이상치가 한개 존재한다면 그 값으로 인해 다른값들이 뭉개질 수도 있다.
1-2-2. Standardization

표준화는 변수의 스케일을 평균이 0, 표준편차가 1이 되도록 변환하는 것이다. 즉 정규분포를 따르게 하는 것이다.
평균에 가까워질수록 0으로, 평균에서 멀어질수록 큰 값으로 변환된다.
표준화는 변수들의 수치범위를 축소시키기 때문에 거리기반 알고리즘에서 장점이 있다.
$$ X_{\text{normalized}} = \frac{X - \mu}{\sigma} $$
1-2-3. Robust scaling

$$ X_{\text{robust scaled}} = \frac{X - Q_1(X)}{Q_3(X) - Q_1(X)} $$
로버스트 스케일링은 평균과 표준편차가 아닌 IQR을 기준으로 스케일링을 진행한다.
중앙값과의 거리를 IQR로 나누어 중앙값에 가까워질수록 0으로, 중앙값에서 멀어질수록 큰 값으로 변환한다. 중앙값을 사용함으로써 이상치에 강건하다는 장점이 있다.
1-3. Binning
구간화는 수치형 변수를 범주형 변수로 전환시키는 방법을 말한다. 범주화시킴으로써 모델의 복잡도가 줄어든다는 장점이 있다.

범주화를 시키는 방법은 크게 두가지가 있는데 등간격과 등빈도가 있다.
등간격은 변수의 동일한 범주를 가지고 범주화를 시키고 등빈도는 같은 개수를 가지도록 범주화를 시킨다. 두 방법 모두 이상치를 완화시킨다는 장점이 있다.
2. 범주형 변수
2-1. One-hot encoding
원-핫 인코딩이란 범주형 변수를 0과 1로만 표현되도록 변환하는 방법이다. 해당 범주형 변수의 총 범주개수만큼의 벡터를 만들고 해당 벡터를 0혹은 1로 채우는 방식이다.
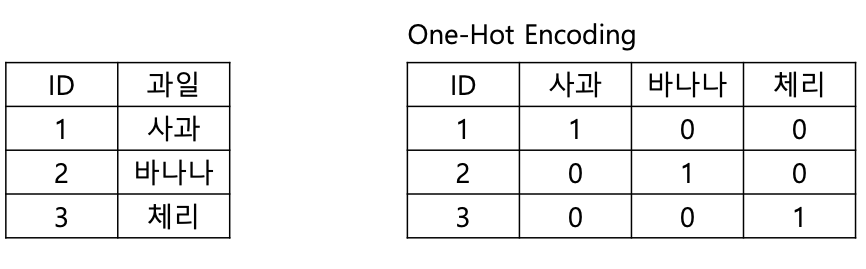
이를 통해 컴퓨터가 변수를 인식할 수 있으며(범주형일경우 인식 불가), 모델이 변수의 의미를 정확하게 파악할 수 있다. 그러나 해당 범주형 변수의 크기만큼 벡터를 생성하는데 해당 값에는 0과 1밖에 들어가지 않기 때문에 희소벡터차원이 늘어나는 문제점이 있다. 이는 메모리 및 연산에 악영향을 주며 차원의 저주가 발생할 수도 있다.
2-2. Label encoding
라벨인코딩은 원-핫인코딩과는 다르게 각 범주를 정수로 표현한다. 따라서 여러 벡터를 만들필요없이 하나의 컬럼으로 모든 범주를 표현가능하다. 특히 순서가 존재하는 범주형 변수일경우 효율적이다.
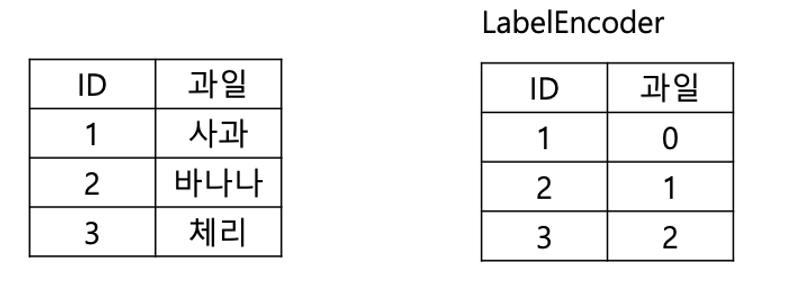
이는 정수로 간단하게 변환할 수 있으며 하나의 변수로 표현 가능하기 때문에 메모리 관리 측면에서 효율적이다.단 변환한 정수를 순서로 인식하게 될수도 있기 때문에 주의하여야 한다. (성적에 해당하는 b,c,a를 라벨인코딩으로 2,1,0 이런식으로 변환하면 잘못된 것)
2-3. Frequency encoding
빈도인코딩은 고유 범주의 빈도값을 이용하여 인코딩하는 방법으로 빈도가 높을 수록 높은 정수값을 빈도가 낮을수록 낮은 정수값을 부여한다. 이는 빈도 정보가 유지된다는 장점이 있으나 다른 특성이라도 빈도가 같다면 같게 변환되어 의미를 동일하게 인식해버릴 수도 있어 주의해야한다.
2-4. Target encoding
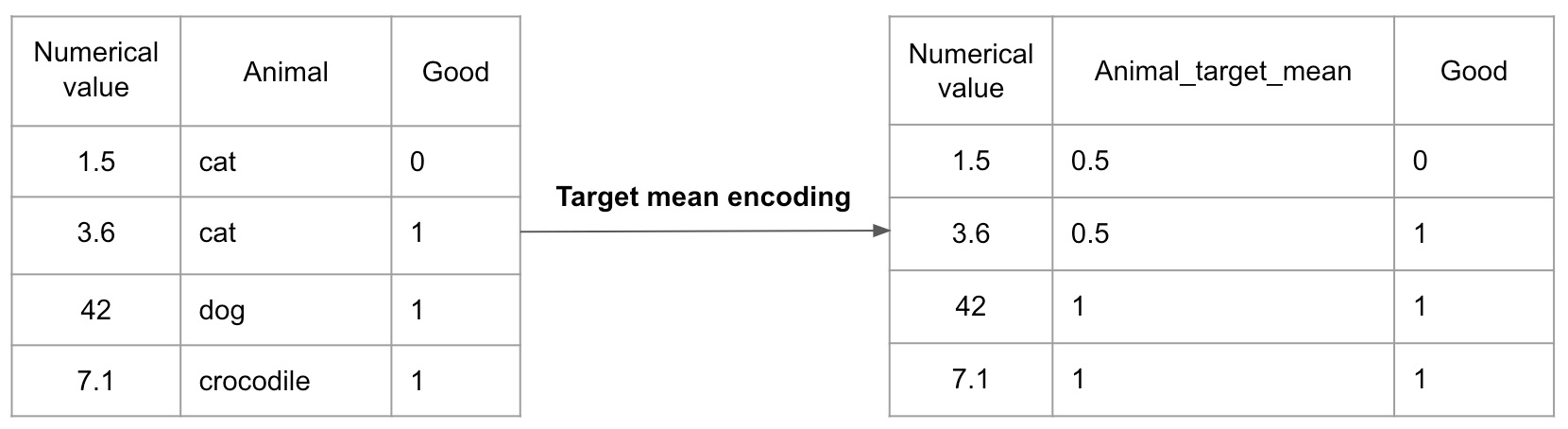
타겟인코딩은 특정 변수를 통계량으로 인코딩하는 방식이다.
범주형 변수를 연속적인 특성을 가진값으로 변환함으로써 특정 타겟변수와 어떤 관련성이 있는지 파악할 수 있다.
이는 범주간의 수치적인 의미를 변수에 부여할 수 있으나 타겟변수에 이상치가 존재하거나 타겟변수의 범주 종류가 소수라면 과적합이 될수도있다. 또한 타겟변수의 특성이 학습 데이터에 노출되는 data-leakage 문제도 조심해야한다.
'ML & DL > 개념정리' 카테고리의 다른 글
| Activation Function: 활성화 함수 (0) | 2024.01.31 |
|---|---|
| Feature engineering (0) | 2024.01.11 |
| 데이터 전처리(이상치&결측치) (0) | 2024.01.10 |
| PyTorch Lightning (0) | 2024.01.09 |
| Hugging Face를 이용한 Finetuning 실습 (0) | 2024.01.09 |
