모델 성능 평가란, 실제값과 모델에 의해 예측된 값의 차이를 구하는 것.
실제값과 예측값이 오차가 0인 것은 실질적으로 힘들기 때문에 오차의 한계를 정해서 그 오차까지는 허용해 준다.
성능평가를 하기 위해서는 예측값과 실제값을 비교할 수 있어야 하기 때문에 지도학습에만 사용된다.
Training set의 결과와 Test set의 결과가 비슷해야 좋은 모델이라고 말할 수 있다.
Training의 성능만 좋게 나왔다면. 이 모델은 과적합된 모델이다.

[Regression]
ex)선형 회귀, Random Regressor -> MSE, RMSE, MAE, MAPE 등의 평가지표 사용
-> 작을수록 성능이 좋음을 의미
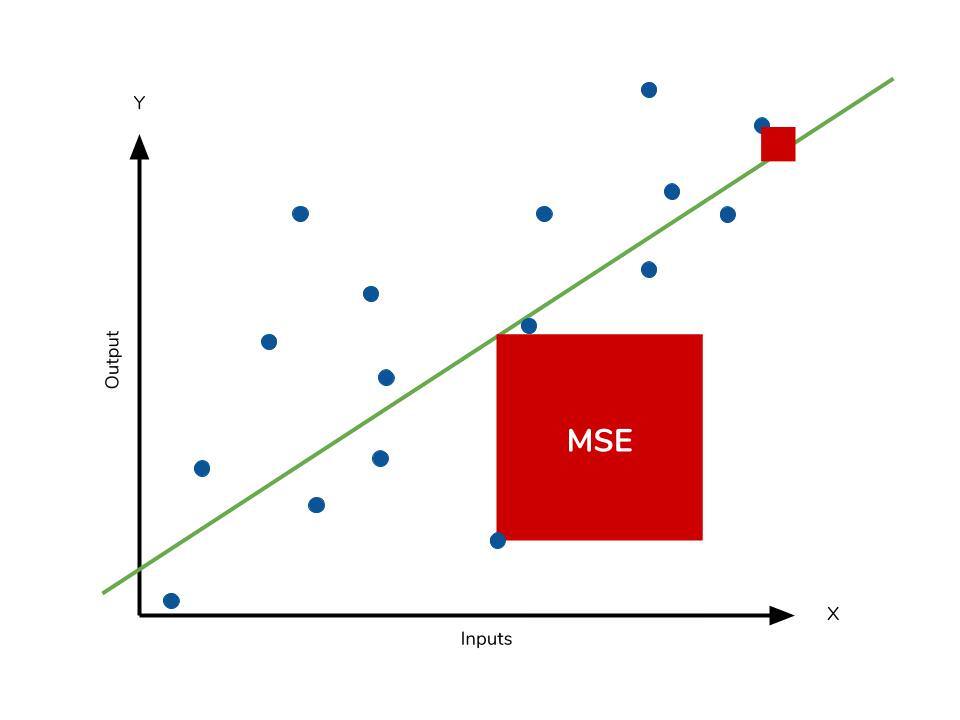
1. MSE
$$ \text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (Y_i - \hat{Y}_i)^2 $$
Mean Squared Error: 잔차(실제값과 예측값의 차이)를 제곱하여 평균한 것.
MSE를 과도하게 줄이면 오버피팅이 될 수 있음.
장점
- 지표 자체가 직관적
단점
- 에측변수와 단위가 다름 (MSE가 4라면, 이 모델은 실제와 예측값의 차이가 평균적으로 2라는 것)
- 스케일에 의존적(데이터의 스케일이 클수록 오차가 크게 보이는 경향이 있다.-제곱하기 때문)
- 잔차를 제곱하기 때문에 이상치에 민감
- 제곱으로 인해 1 미만의 에러는 더 작아지고, 1 이상의 에러는 더 증가하는 오차의 왜곡이 존재
- 잔차에 제곱을 하기 때문에 실제값에 대해 과소평가인지 과대평가인지 알 수 없음.
2. RMSE
$$ \text{RMSE} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (Y_i - \hat{Y}_i)^2} $$
MSE의 제곱근으로, MSE가 오류의 제곱을 구하게 되어 실제 오류의 평균보다 커지는 특성이 있어 이를 방지하기 위해 제곱근을 취한 것.
큰 오류값 차이에 대하여 크게 페널티를 준다.
장점
- 지표자체가 직관적이며 예측변수와 단위가 같다. (MSE는 제곱이 되어있음)
- 제곱된 잔차를 풀어주기 때문에 값의 왜곡이 덜하다.
단점
- 실제값에 대해 과소평가인지 과대평가인지 알 수 없음.
- 스케일에 의존적이다.
- 이상치에 민감하다.
3. RMSLE
$$\text{RMSLE} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (\log(1 + y_i) - \log(1 + \hat{y}_i))^2}$$
RMSE에 로그를 취해준 형태. log 0은 무한대로 수렴하기 때문에 +1을 해주었음.
과소측정에 큰 페널티를 부여한다. 즉 예측값이 실제값보다 작을 때 큰 페널티를 부여한다.
장점
- 이상치에 강건하다.
- 상대적인 error을 측정해 준다.
4. R2 , R squared
다른 지표들은 데이터에 따라 값의 스케일이 다르기 때문에 절댓값만 보고 성능을 판단하기 어렵다.
이때 R2 score은 상대적인 성능을 나타내기에 비교가 쉽다. - 종속변수에 대한 설명변수의 설명력을 알고자 할 때 사용.
실제값의 분산 대비 예측값의 분산 비율을 의미하며 1에 가까울수록 좋다.
SST는 전체 제곱합(실제 관측치와 y값들의 평균의 차이를 제곱하여 합한 값)
SSR은 회귀 제곱합(예측치와 y값들의 평균의 차이를 제곱하여 합한 값)
SSE는 오차제곱합(실제 관측치와 예측의 차이를 제곱하여 합한 값)
- 단, 독립변수가 많아질수록 R이 커지기 때문에 단순 R만 봐서도 안된다
$$ R^2 = 1 - \frac{\sum_{i=1}^{n} (Y_i - \hat{Y}_i)^2}{\sum_{i=1}^{n} (Y_i - \bar{Y})^2}=1-\frac{\text{SSE}}{\text{SST}}$$
4. MAE
$$ \text{MAE} = \frac{1}{n} \sum_{i=1}^{n} \left| y_i - \hat{y}_i \right| $$
절대 평균오차라고 부르며, 실제값과 예측값 사이의 절대적인 오차의 평균.
장점
- 지표자체가 직관적이고, 예측변수와 단위가 같다. (MAE=2라면, 실제와 예측값의 차이가 평균적으로 2라는 것)
- MSE에 비해 이상치에 robust함.
단점
- 잔차에 절대값을 씌우기 때문에 실제값에 대하여 과소평가인지 과대평가인지 알 수 없음.
- 스케일에 의존적이다.(A의 실제값이 100, 예측값이 90이고 B의 실제값이 1000 예측값이 990이라고 할 때 둘 다 MAE는 10인데 오차 비율은 다름)

5. MAPE
$$ \text{MAPE} = \frac{1}{n} \sum_{i=1}^{n} \left| \frac{y_i - \hat{y}_i}{y_i} \right| \times 100 $$
MAE를 비율로 표현한 것.
쉽게 말하자면 실제값 대비 얼마나 예측값의 차이가 있는지를 백분율로 표현한 것
장점
- 지표자체가 직관적이다.
- 스케일에 의존적이지 않다.
단점
- 실제값에 대해 과소평가인지 과대평가인지 알 수 없음.
- 비율로 해석이 의미있는 값에만 적용됨(하락/상승률 같은 데에는 적합하지만, 수치에 대한 비교에는 쓸모가 없음)
- 실제값에 0이 있는 경우 계산할 수 없음.

[Classification]
우선 알아둬야 할 것이 positive, negative는 맞다 틀리다를 나타내는 것이 아니라 양성. 음성의 개념이라고 생각해야 한다. positive가 좋은 것이고, negative가 틀린 것이 아니다.
우선 아래의 표를 `Confusion matrix` 라고 부른다.

1. 정확도(Accuracy)
전체데이터 중에 정확하게 예측한 데이터 수 ( 정확하게 예측할 때 답이 Positive든 Negative든 상관없다)
불균형한 레이블 데이터 셋에서 매우 좋지 못한 예측을 한다.
-> 모든 분류 건수 중에서 분류기가 몇 개의 정답을 맞혔는가 (맞거나 틀리다고 정확히 분류했는가)
TP= 양성을 양성으로 예측한 것, FN=음성을 음성으로 예측한 것
$$ \text{Accuracy} = \frac{TP + TN}{TP + TN + FP + FN} $$
2. 정밀도(Precision)
Positive로 예측한 것 중 실제로 맞춘 비율
=분류기가 Positive로 분류한 것 중에서 실제로 Positive인 개수
$$\text{Precision} = \frac{TP}{TP + FP}$$
Positive 예측 성능을 더욱 정밀하게 측정하기 위한 평가 지표.
1에 가까울 수록 이상적 (FP를 낮추는 것에 집중)
- FP: 스팸메일이 아닌데(양성), 스팸메일(음성)이라고 판단 / FN: 스팸메일(음성)인데 스팸메일이 아니(양성)라고 판단
여기서는 스팸메일이 아닌데 스펨메일이 돼버리는 게 더 안 좋은 결과이므로 FP를 낮추려고 한다.
3. 재현율(Recall)
실제 Positive를 얼마나 잘 예측했는지를 나타내는 지표
== 실제 Positve인 것 중에서 분류기가 Positive로 분류한 개수
$$\text{Recall} = \frac{TP}{TP + FN}$$
1에 가까울수록 이상적 (FN을 낮추는 것에 집중)
- FP: 암이 아닌 환자에게 암진단 / FN: 암인 환자에게 암이 아니라고 진단
여기서는 암인 환자에게 암이 아니라고 진단하는 것이 더 치명적인 결과이므로 FN을 낮추고자 한다.
4. F1-score
$$ F1 = 2 \times \frac{\text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}} $$
Recall과 Precision을 이용하여 조화평균을 구한 지표
Recall과 Precision은 trade-off 의 관계이므로, 이 둘을 적절히 사용하기 위해서 F1-score이 존재
불균형 분류 문제에서 평가 지표로 주로 사용
정밀도와 재현율 어느 한쪽으로 치우치지 않는 수치를 나타낼 때 F1 score는 상대적으로 높은 값을 가짐
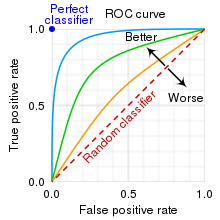
5. ROC curve
다양한 thresh hold에서의 성능을 한 눈에 볼 수 있도록 시각화 한 측정 그래프
- x축을 FPR, y축을 TPR로 갖는 그래프
좌상단에 치우칠수록 높은 성능을 의미한다.
정리
True Positive: 실제 Positive인 정답을 Positive라고 예측 (True)
True Negative: 실제 Negative인 정답을 Negative라고 예측 (True)
False Positive: 실제 Negative인 정답을 Positive라고 예측 (False) – Type I error
False Negative: 실제 Positive인 정답을 Negative라고 예측 (False) – Type II error
앞에 오는 True, False는 예측이 맞았는지 틀렸는지를 나타내고,
뒤에 오는 Positive, Negative는 실제 예측이 양성인지 음성인지를 나타냄.
'ML & DL > 개념정리' 카테고리의 다른 글
| Decision Tree:의사결정나무 (0) | 2023.12.13 |
|---|---|
| 분류와 회귀 (0) | 2023.12.11 |
| 부스팅(Boosting) 알고리즘 (0) | 2023.11.30 |
| Clustering: 클러스터링 (0) | 2023.11.28 |
| 머신러닝 기초 (0) | 2023.11.24 |
